Interpretability

ACTL3143 & ACTL5111 Deep Learning for Actuaries

Patrick Laub

Introduction

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

Definitions

“Surprisingly enough, although the concept of interpretability is increasingly widespread, there is no general consensus on both the definition and the measurement of the interpretability of a model.” (Delcaillau et al. 2022)

“Definition Interpret means to explain or to present in understandable terms. In the context of ML systems, we define interpretability as the ability to explain or to present in understandable terms to a human.” (Doshi-Velez and Kim 2017)

A distinction between interpretability and explainability

“Interpretability is about transparency, about understanding exactly why and how the model is generating predictions, and therefore, it is important to observe the inner mechanics of the algorithm considered. This leads to interpreting the model’s parameters and features used to determine the given output. Explainability is about explaining the behavior of the model in human terms.” (Charpentier 2024)

Aspects of Interpretability

Inherent Interpretability

The model is interpretable by design.

Post-hoc Explanations

The model is not interpretable by design, but we can use other methods to explain the model.

Global Interpretability

The ability to understand how the model works.

Local Interpretability

The ability to interpret/understand each prediction.

Husky vs. Wolf

A well-known anecdote in the explainability literature (Ribeiro, Singh, and Guestrin 2016).

Adversarial examples

A demonstration of fast adversarial example generation applied to GoogLeNet on ImageNet. By adding an imperceptibly small vector whose elements are equal to the sign of the elements of the gradient of the cost function with respect to the input, we can change GoogLeNet’s classification of the image (Goodfellow, Shlens, and Szegedy 2014)

Adversarial stickers

Adversarial stickers.

Adversarial text

“TextAttack 🐙 is a Python framework for adversarial attacks, data augmentation, and model training in NLP”

Demo

LLMs are even more opaque

“Figure 1: An overview of our research from generating to evaluating EmotionPrompt.” (Li et al. 2023)

A popular science article about Ben-Zion et al. (2025)

Illustrative Example

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

First attempt at NLP task

df_raw = pd.read_parquet("../Natural-Language-Processing/NHTSA_NMVCCS_extract.parquet.gzip")

df_raw["NUM_VEHICLES"] = df_raw["NUMTOTV"].map(lambda x: str(x) if x <= 2 else "3+")

weather_cols = [f"WEATHER{i}" for i in range(1, 9)]
features = df_raw[["SUMMARY_EN"] + weather_cols]

target_labels = df_raw["NUM_VEHICLES"]
target = LabelEncoder().fit_transform(target_labels)

X_main, X_test, y_main, y_test = train_test_split(features, target, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(X_main, y_main, test_size=0.25, random_state=1)

df_raw["SUMMARY_EN"]

0       V1, a 2000 Pontiac Montana minivan, made a lef...
1       The crash occurred in the eastbound lane of a ...
2       This crash occurred just after the noon time h...
                              ...                        
6946    The crash occurred in the eastbound lanes of a...
6947    This single-vehicle crash occurred in a rural ...
6948    This two vehicle daytime collision occurred mi...
Name: SUMMARY_EN, Length: 6949, dtype: object

df_raw["NUM_VEHICLES"].value_counts()\
  .sort_index()

NUM_VEHICLES
1     1822
2     4151
3+     976
Name: count, dtype: int64

Bag of words for the top 1,000 words

def vectorise_dataset(X, vect, txt_col="SUMMARY_EN", dataframe=False):
    X_vects = vect.transform(X[txt_col]).toarray()
    X_other = X.drop(txt_col, axis=1)

    if not dataframe:
        return np.concatenate([X_vects, X_other], axis=1)                           
    else:
        # Add column names and indices to the combined dataframe.
        vocab = list(vect.get_feature_names_out())
        X_vects_df = pd.DataFrame(X_vects, columns=vocab, index=X.index)
        return pd.concat([X_vects_df, X_other], axis=1) 

vect = CountVectorizer(max_features=1_000, stop_words="english")
vect.fit(X_train["SUMMARY_EN"])

X_train_bow = vectorise_dataset(X_train, vect)
X_val_bow = vectorise_dataset(X_val, vect)
X_test_bow = vectorise_dataset(X_test, vect)

vectorise_dataset(X_train, vect, dataframe=True).head()

	10	105	113	12	15	150	16	17	18	180	...	yield	zone	WEATHER1	WEATHER2	WEATHER3	WEATHER4	WEATHER5	WEATHER6	WEATHER7	WEATHER8
2532	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
6209	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
2561	1	0	1	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
6664	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
4214	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 1008 columns

Trained a basic neural network on that

def build_model(num_features, num_cats):
    random.seed(42)
    
    model = Sequential([
        Input((num_features,)),
        Dense(100, activation="relu"),
        Dense(num_cats, activation="softmax")
    ])
    
    topk = SparseTopKCategoricalAccuracy(k=2, name="topk")
    model.compile("adam", "sparse_categorical_crossentropy",
        metrics=["accuracy", topk])
    
    return model

num_features = X_train_bow.shape[1]
num_cats = df_raw["NUM_VEHICLES"].nunique()
model = build_model(num_features, num_cats)
es = EarlyStopping(patience=1, restore_best_weights=True, monitor="val_accuracy")
model.fit(X_train_bow, y_train, epochs=10,
    callbacks=[es], validation_data=(X_val_bow, y_val), verbose=0)
model.summary()

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense (Dense)                   │ (None, 100)            │       100,900 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 3)              │           303 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 303,611 (1.16 MB)

 Trainable params: 101,203 (395.32 KB)

 Non-trainable params: 0 (0.00 B)

 Optimizer params: 202,408 (790.66 KB)

model.evaluate(X_train_bow, y_train, verbose=0)

[0.021850384771823883, 0.9992803931236267, 1.0]

model.evaluate(X_val_bow, y_val, verbose=0)

[3.338824987411499, 0.9762589931488037, 0.9971222877502441]

Permutation importance algorithm

Taken directly from scikit-learn documentation:

• Inputs: fitted predictive model m, tabular dataset (training or validation) D.

• Compute the reference score s of the model m on data D (for instance the accuracy for a classifier or the R^2 for a regressor).

• For each feature j (column of D):

  • For each repetition k in {1, \dots, K}:

    • Randomly shuffle column j of dataset D to generate a corrupted version of the data named \tilde{D}_{k,j}.
    • Compute the score s_{k,j} of model m on corrupted data \tilde{D}_{k,j}.

  • Compute importance i_j for feature f_j defined as:

    i_j = s - \frac{1}{K} \sum_{k=1}^{K} s_{k,j}

def permutation_test(model, X, y, num_reps=1, seed=42):
    """
    Run the permutation test for variable importance.
    Returns matrix of shape (X.shape[1], len(model.evaluate(X, y))).
    """
    rnd.seed(seed)
    scores = []    

    for j in range(X.shape[1]):
        original_column = np.copy(X[:, j])
        col_scores = []

        for r in range(num_reps):
            rnd.shuffle(X[:,j])
            col_scores.append(model.evaluate(X, y, verbose=0))

        scores.append(np.mean(col_scores, axis=0))
        X[:,j] = original_column
    
    return np.array(scores)

Run the permutation test

all_perm_scores = permutation_test(model, X_val_bow, y_val)

perm_scores = all_perm_scores[:,1]
plt.plot(perm_scores)
plt.xlabel("Input index")
plt.ylabel("Accuracy when shuffled");

Find the most significant inputs

vocab = vect.get_feature_names_out()
input_cols = list(vocab) + weather_cols

best_input_inds = np.argsort(perm_scores)[:100]
best_inputs = [input_cols[idx] for idx in best_input_inds]

print(best_inputs)

['v3', 'v2', 'vehicle', 'lane', 'harmful', 'right', 'divided', 'south', 'motor', 'dry', 'event', 'left', 'parked', 'WEATHER4', 'related', 'stop', 'impact', 'v4', 'crash', 'direction', 'involved', 'internal', 'stated', 'barrier', 'dodge', 'asphalt', 'chevrolet', 'higher', 'forward', 'pre', 'precrash', 'pushed', 'corner', 'hand', 'prior', 'door', 'WEATHER8', 'factor', 'work', 'mph', 'year', 'critical', 'WEATHER1', 'WEATHER3', 'single', 'WEATHER5', 'straight', 'ahead', 'turning', 'honda', 'hours', 'type', 'daylight', 'possible', 'ford', 'male', 'facing', 'actions', 'consists', 'unknown', 'uphill', 'pick', 'stopped', 'point', 'alcohol', 'high', 'pull', 'proceeded', 'encroaching', 'morning', 'trailer', 'grand', 'associated', 'blood', 'meters', 'basis', 'experience', 'prescription', 'moved', 'small', 'steered', 'maneuver', 'medication', 'heart', 'rotate', 'old', 'pain', 'weekday', 'clear', 'seconds', 'civic', 'started', 'northbound', '2006', 'noon', 'miles', '44', 'injuries', 'vehicles', 'saw']

How about a simple decision tree?

from sklearn import tree

clf = tree.DecisionTreeClassifier(random_state=0, max_leaf_nodes=3)
clf.fit(X_train_bow[:, best_input_inds], y_train);

print(clf.score(X_train_bow[:, best_input_inds], y_train))
print(clf.score(X_val_bow[:, best_input_inds], y_val))

0.9275605660829935
0.939568345323741

The decision tree ends up giving pretty good results.

Decision tree

tree.plot_tree(clf, feature_names=best_inputs, filled=True);

print(np.where(clf.feature_importances_ > 0)[0])
[best_inputs[ind] for ind in np.where(clf.feature_importances_ > 0)[0]]

[ 0 41]

['v3', 'critical']

This is why we replace “v1”, “v2”, “v3”

# Go through every summary and find the words "V1", "V2" and "V3".
# For each summary, replace "V1" with a random number like "V1623", and "V2" with a different random number like "V1234".
rnd.seed(123)

df = df_raw.copy()
for i, summary in enumerate(df["SUMMARY_EN"]):
    word_numbers = ["one", "two", "three", "four", "five", "six", "seven", "eight", "nine", "ten"]
    num_cars = 10
    new_car_nums = [f"V{rnd.randint(100, 10000)}" for _ in range(num_cars)]
    num_spaces = 4

    for car in range(1, num_cars+1):
        new_num = new_car_nums[car-1]
        summary = summary.replace(f"V-{car}", new_num)
        summary = summary.replace(f"Vehicle {word_numbers[car-1]}", new_num).replace(f"vehicle {word_numbers[car-1]}", new_num)
        summary = summary.replace(f"Vehicle #{word_numbers[car-1]}", new_num).replace(f"vehicle #{word_numbers[car-1]}", new_num)
        summary = summary.replace(f"Vehicle {car}", new_num).replace(f"vehicle {car}", new_num)
        summary = summary.replace(f"Vehicle #{car}", new_num).replace(f"vehicle #{car}", new_num)
        summary = summary.replace(f"Vehicle # {car}", new_num).replace(f"vehicle # {car}", new_num)

        for j in range(num_spaces+1):
            summary = summary.replace(f"V{' '*j}{car}", new_num).replace(f"V{' '*j}#{car}", new_num).replace(f"V{' '*j}# {car}", new_num)
            summary = summary.replace(f"v{' '*j}{car}", new_num).replace(f"v{' '*j}#{car}", new_num).replace(f"v{' '*j}# {car}", new_num)
         
    df.loc[i, "SUMMARY_EN"] = summary

There was a slide in the NLP deck titled “Just ignore this for now…” That was going through each summary and replacing the words “V1”, “V2”, “V3” with random numbers. This was done to see if the model was overfitting to these words.

features = df[["SUMMARY_EN"] + weather_cols]
X_main, X_test, y_main, y_test = train_test_split(features, target, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(X_main, y_main, test_size=0.25, random_state=1)

vect = CountVectorizer(max_features=1_000, stop_words="english")
vect.fit(X_train["SUMMARY_EN"])

X_train_bow = vectorise_dataset(X_train, vect)
X_val_bow = vectorise_dataset(X_val, vect)
X_test_bow = vectorise_dataset(X_test, vect)

model = build_model(num_features, num_cats)

es = EarlyStopping(patience=1, restore_best_weights=True,
    monitor="val_accuracy", verbose=2)

model.fit(X_train_bow, y_train, epochs=10,
    callbacks=[es], validation_data=(X_val_bow, y_val), verbose=0);

Retraining on the fixed dataset gives us a more realistic (lower) accuracy.

model.evaluate(X_train_bow, y_train, verbose=0)

[0.1021684780716896, 0.9815303683280945, 0.9990405440330505]

model.evaluate(X_val_bow, y_val, verbose=0)

[2.4335880279541016, 0.9381294846534729, 0.9942445755004883]

Permutation importance accuracy plot

perm_scores = permutation_test(model, X_val_bow, y_val)[:,1]
plt.plot(perm_scores)
plt.xlabel("Input index"); plt.ylabel("Accuracy when shuffled");

Find the most significant inputs

vocab = vect.get_feature_names_out()
input_cols = list(vocab) + weather_cols

best_input_inds = np.argsort(perm_scores)[:100]
best_inputs = [input_cols[idx] for idx in best_input_inds]

print(best_inputs)

['involved', 'harmful', 'event', 'struck', 'motor', 'higher', 'direction', 'line', 'ford', 'edge', 'single', 'lane', 'contacted', 'left', 'old', 'parked', 'vehicle', 'turned', 'guardrail', 'injured', 'coded', 'legally', 'encroachment', 'critical', 'associated', 'driving', 'intersection', 'location', 'traffic', 'limit', 'rear', 'pushed', 'police', 'stopped', 'include', 'approaching', 'WEATHER5', 'brakes', 'clear', 'WEATHER4', 'way', 'continued', 'counterclockwise', 'turning', 'hit', 'departed', 'driven', 'afternoon', 'northwest', 'stop', 'steered', 'female', 'saw', 'passenger', 'pickup', 'truck', 'actions', 'WEATHER8', '1993', 'properly', 'sky', 'roof', 'sleep', 'road', 'causing', 'approached', 'applied', 'mercury', 'tree', '23', 'possible', 'large', 'check', 'wearing', 'advisory', 'later', 'door', 'divided', 'distraction', '2006', 'treated', 'travels', 'green', 'gmc', 'past', 'path', 'initial', 'final', 'school', 'towed', 'tire', 'time', 'crossing', 'unsuccessful', 'outside', 'route', 'unable', 'adjacent', 'moved', 'southbound']

Inherently Interpretable Models

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

What is inherent interpretability?

“Interpretability by design is decided on the level of the machine learning algorithm. If you want a machine learning algorithm that produces interpretable models, the algorithm has to constrain the search of models to those that are interpretable. The simplest example is linear regression: When you use ordinary least squares to fit/train a linear regression model, you are using an algorithm that will produce … models that are linear in the input features. Models that are interpretable by design are also called intrinsically or inherently interpretable models.” (Molnar 2020)

Christoph Molnar

Examples of interpretable models

• Linear regression
• Generalised linear models
• Decision trees
• Decision rules

graph TD
  A{vpdmax8 < 27}
  A -->|true| B{pcpn8 ≥ 37}
  A -->|false| C{vpdmax6 < 29}

  B -->|true| D{tmax9 ≥ 21}
  B -->|false| E{tmax6 ≥ 26}

  D -->|true| F[11]
  D -->|false| G[118]

  E -->|true| H[60]
  E -->|false| I[133]

  C -->|true| J{tmax7 ≥ 31}
  C -->|false| M{tmax7 < 31}

  J -->|true| K[81]
  J -->|false| L[131]

  M -->|true| N[82]
  M -->|false| O[186]

E.g. decision tree for payouts of index insurance (Chen et al. 2024).

Better trees

“The optimization over the node parameters (exact for axis-aligned trees, approximate for oblique trees) assumes the rest of the tree (structure and parameters) is fixed. The greedy nature of the algorithm means that once a node is optimized, it its fixed forever.” (Carreira-Perpinán and Tavallali 2018)

Non-greedy search can improve the accuracy of the tree, without sacrificing interpretability.

Some processes don’t fit the tree structure

Train prices

Full train pricing

Decision rules

Make predictions using if-then statements related to the inputs.

“Decision rules can be as expressive as decision trees, while being more compact. Decision trees often also suffer from replicated sub-trees, that is, when the splits in a left and a right child node have the same structure.” (Molnar 2020)

def rail_cost(peak_hours, distance):
  if peak_hours:
      if distance <= 10:
        cost = 3.79
      elif distance <= 20:
        cost = 4.71
      elif distance <= 35:
        cost = 5.42
      elif distance <= 65:
        cost = 7.24
      else:
        cost = 9.31
  else:
      if distance <= 10:
        cost = 2.65
      elif distance <= 20:
        cost = 3.29
      elif distance <= 35:
        cost = 3.79
      elif distance <= 65:
        cost = 5.06
      else:
        cost = 6.51
  return cost

Scoring rules

Example from Rudin (2019).

When to choose inherent interpretability?

Rudin (2019)

Cynthia Rudin

Article 22 GDPR – Automated individual decision-making, including profiling

1. The data subject shall have the right not to be subject to a decision based solely on automated processing, including profiling, which produces legal effects concerning him or her or similarly significantly affects him or her.

2. Paragraph 1 shall not apply if the decision:

   1. is necessary for entering into, or performance of, a contract between the data subject and a data controller;
      
   2. is authorised by Union or Member State law to which the controller is subject and which also lays down suitable measures to safeguard the data subject’s rights and freedoms and legitimate interests; or
      
   3. is based on the data subject’s explicit consent.

3. In the cases referred to in points (a) and (c) of paragraph 2, the data controller shall implement suitable measures to safeguard the data subject’s rights and freedoms and legitimate interests, at least the right to obtain human intervention on the part of the controller, to express his or her point of view and to contest the decision.

4. Decisions referred to in paragraph 2 shall not be based on special categories of personal data referred to in Article 9(1), unless point (a) or (g) of Article 9(2) applies and suitable measures to safeguard the data subject’s rights and freedoms and legitimate interests are in place.

Linear models & LocalGLMNet

A GLM has the form

\hat{y} = g^{-1}\bigl( \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p \bigr)

where \beta_0, \dots, \beta_p are the model parameters.

Global & local interpretations are easy to obtain.

LocalGLMNet extends this to a neural network (Richman and Wüthrich 2023).

\hat{y_i} = g^{-1}\bigl( \beta_0(\boldsymbol{x}_i) + \beta_1(\boldsymbol{x}_i) x_{i1} + \dots + \beta_p(\boldsymbol{x}_i) x_{ip} \bigr)

A GLM with local parameters \beta_0(\boldsymbol{x}_i), \dots, \beta_p(\boldsymbol{x}_i) for each observation \boldsymbol{x}_i. The local parameters are the output of a neural network.

Neural Additive Models (NAMs)

Each covariate (or select interactions) receive their own subnetwork, which contribute additively.

Post-hoc Explanations

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

One variable’s effect on the prediction

Various plots showing the effect of one variable on the prediction; from (Molnar 2020, sec. 12)

The different plots

A Ceteris Paribus plot shows how the model’s prediction changes as we vary the value of one covariate/input while keeping all other features constant at their original values for some observation.

An Individual Conditional Expectation (ICE) plot is the same thing as a ceteris paribus plot, but for each observation in the dataset.

A Partial Dependence Plot (PDP) shows how the model’s prediction changes as we vary the value of one covariate/input while averaging over all other features in the dataset.

Useful for Hyperparameter Tuning

Partial dependence plots for hyperparameter tuning

Permutation importance

• Inputs: fitted model m, tabular dataset D.

• Compute the reference score s of the model m on data D (for instance the accuracy for a classifier or the R^2 for a regressor).

• For each feature j (column of D):

  • For each repetition k in {1, \dots, K}:

    • Randomly shuffle column j of dataset D to generate a corrupted version of the data named \tilde{D}_{k,j}.
    • Compute the score s_{k,j} of model m on corrupted data \tilde{D}_{k,j}.

  • Compute importance i_j for feature f_j defined as:

    i_j = s - \frac{1}{K} \sum_{k=1}^{K} s_{k,j}

Originally proposed by Breiman (2001), extended by Fisher, Rudin, and Dominici (2019).

Permutation importance

def permutation_test(model, X, y, num_reps=1, seed=42):
    """
    Run the permutation test for variable importance.
    Returns matrix of shape (X.shape[1], len(model.evaluate(X, y))).
    """
    rnd.seed(seed)
    scores = []    

    for j in range(X.shape[1]):
        original_column = np.copy(X[:, j])
        col_scores = []

        for r in range(num_reps):
            rnd.shuffle(X[:,j])
            col_scores.append(model.evaluate(X, y, verbose=0))

        scores.append(np.mean(col_scores, axis=0))
        X[:,j] = original_column
    
    return np.array(scores)

LIME

Local Interpretable Model-agnostic Explanations employs an interpretable surrogate model to explain locally how the black-box model makes predictions for individual instances.

E.g. a black-box model predicts Bob’s premium as the highest among all policyholders. LIME uses an interpretable model (a linear regression) to explain how Bob’s features influence the black-box model’s prediction.

LIME Algorithm

Suppose we want to explain the instance \boldsymbol{x}_{\text{Bob}}=(1, 2, 0.5).

1. Generate perturbed examples of \boldsymbol{x}_{\text{Bob}} and use the trained gamma MDN f to make predictions: \begin{align*} \boldsymbol{x}^{'(1)}_{\text{Bob}} &= (1.1, 1.9, 0.6), \quad f\big(\boldsymbol{x}^{'(1)}_{\text{Bob}}\big)=34000 \\ \boldsymbol{x}^{'(2)}_{\text{Bob}} &= (0.8, 2.1, 0.4), \quad f\big(\boldsymbol{x}^{'(2)}_{\text{Bob}}\big)=31000 \\ &\vdots \quad \quad \quad \quad\quad \quad\quad \quad\quad \quad \quad \vdots \end{align*} We can then construct a dataset of N_{\text{Examples}} perturbed examples: \mathcal{D}_{\text{LIME}} = \big(\big\{\boldsymbol{x}^{'(i)}_{\text{Bob}},f\big(\boldsymbol{x}^{'(i)}_{\text{Bob}}\big)\big\}\big)_{i=0}^{N_{\text{Examples}}}.

LIME Algorithm

2. Fit an interpretable model g, i.e., a linear regression using \mathcal{D}_{\text{LIME}} and the following loss function: \mathcal{L}_{\text{LIME}}(f,g,\pi_{\boldsymbol{x}_{\text{Bob}}})=\sum_{i=1}^{N_{\text{Examples}}}\pi_{\boldsymbol{x}_{\text{Bob}}}\big(\boldsymbol{x}^{'(i)}_{\text{Bob}}\big)\cdot \bigg(f\big(\boldsymbol{x}^{'(i)}_{\text{Bob}}\big)-g\big(\boldsymbol{x}^{'(i)}_{\text{Bob}}\big)\bigg)^2, where \pi_{\boldsymbol{x}_{\text{Bob}}}\big(\boldsymbol{x}^{'(i)}_{\text{Bob}}\big) represents the distance from the perturbed example \boldsymbol{x}^{'(i)}_{\text{Bob}} to the instance to be explained \boldsymbol{x}_{\text{Bob}}.

“Explaining” to Bob

The bold red cross is the instance being explained. LIME samples instances (grey nodes), gets predictions using f (gamma MDN) and weighs them by the proximity to the instance being explained (represented here by size). The dashed line g is the learned local explanation.

“Again the approximation must be imperfect, otherwise one would throw out the black box and instead use the explanation as an inherently interpretable model.” (Rudin et al. 2022)

SHAP Values

The SHapley Additive exPlanations (SHAP) value helps to quantify the contribution of each feature to the prediction for a specific instance (Lundberg and Lee 2017).

The SHAP value for the jth feature is defined as \begin{align*} \text{SHAP}^{(j)}(\boldsymbol{x}) &= \sum_{U\subset \{1, ..., p\} \backslash \{j\}} \frac{1}{p} \binom{p-1}{|U|}^{-1} \big(\mathbb{E}[Y| \boldsymbol{x}^{(U\cup \{j\})}] - \mathbb{E}[Y|\boldsymbol{x}^{(U)}]\big), \end{align*} where p is the number of features. A positive SHAP value indicates that the variable increases the prediction value.

SHAP waterfall plot

SHAP waterfall plot

Belgian Motor Dataset

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

beMTPL97 dataset

data = pd.read_csv('data/raw/beMTPL97.csv')
claims = data.drop(columns = ["id", "claim", "amount", "average"])
claims.shape

(163212, 14)

postcode = claims.pop("postcode")
train_raw, test_raw = train_test_split(claims, test_size=0.2, random_state=2000, stratify=postcode)

X_train_raw = train_raw.drop(columns='nclaims')
X_test_raw = test_raw.drop(columns='nclaims')
y_train_raw = train_raw['nclaims']
y_test_raw = test_raw['nclaims']

num_vars = ['expo', 'ageph', 'bm', 'power', 'agec', 'lat', 'long']
cat_vars = ['coverage', 'sex', 'fuel', 'use', 'fleet']

Covariates

Numerical variables:

Variable	Description
expo	exposure to risk.
ageph	policyholder’s age.
bm	An integer for the level on the former Belgian bonus-malus scale (0 to 22; higher = worse claims history).
power	vehicle’s horsepower in kilowatts.
agec	vehicle’s age in years.
long	longitude of the policyholder’s municipality center.
lat	latitude of the policyholder’s municipality center.

Target is nclaims.

Categorical variables:

Variable	Description
coverage	insurance coverage level: "TPL" (third party liability), "TPL+" (TPL + limited material damage), "TPL++" (TPL + comprehensive material damage).
sex	policyholder’s gender: "female", "male".
bm	level on the former Belgian bonus-malus scale (0 to 22; higher = worse claims history).
fuel	vehicle’s fuel type: "gasoline" or "diesel".
use	vehicle’s use: "private" or "work".
fleet	vehicle is part of a fleet (1 = yes, 0 = no).

Exposure & frequency

claims["expo"].plot(kind='hist', title='Exposure Distribution')

claims["nclaims"].value_counts()

nclaims
0    144936
1     16539
2      1556
3       162
4        17
5         2
Name: count, dtype: int64

Map of claims

import geopandas as gpd
import contextily as ctx
from shapely.geometry import Point

# Compute average claims per location
avg = train_raw.groupby(['lat', 'long'], as_index=False)['nclaims'].mean()

# Build GeoDataFrame in Web Mercator
gdf = gpd.GeoDataFrame(
    avg,
    geometry=[Point(xy) for xy in zip(avg.long, avg.lat)],
    crs="EPSG:4326"
).to_crs(epsg=3857)

# Plot
ax = gdf.plot(
    column='nclaims',
    cmap='OrRd',
    markersize=8,
    edgecolor='grey',
    linewidth=0.5,
    alpha=0.8,
    legend=True,
    figsize=(10, 5)
)
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
ax.set_axis_off()
plt.title("Average Claims per Location")
plt.show()

Fitting using statsmodels

import statsmodels.api as sm
import statsmodels.formula.api as smf

formula = "nclaims ~ expo + ageph + bm + power + agec + lat + long " + \
    " + C(coverage) + C(sex) + C(fuel) + C(use) + C(fleet)"

glm_model = smf.glm(
    formula=formula,
    data=train_raw,
    family=sm.families.Poisson()
).fit()

Question

What do you expect to be the relationship between ageph and nclaims?

X_train_first = X_train_raw.iloc[0:1].copy()
X_train_first

	expo	coverage	ageph	sex	bm	power	agec	fuel	use	fleet	long	lat
25776	1.0	TPL	59	female	0	51	15	gasoline	private	0	4.387146	51.216042

Summary

glm_model.summary().tables[0]

Generalized Linear Model Regression Results

Dep. Variable:	nclaims	No. Observations:	130569
Model:	GLM	Df Residuals:	130555
Model Family:	Poisson	Df Model:	13
Link Function:	Log	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-49908.
Date:	Wed, 30 Jul 2025	Deviance:	69690.
Time:	23:00:35	Pearson chi2:	1.39e+05
No. Iterations:	6	Pseudo R-squ. (CS):	0.01842
Covariance Type:	nonrobust

Summary

glm_model.summary().tables[1]

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	-7.0204	1.344	-5.222	0.000	-9.655	-4.386
C(coverage)[T.TPL+]	-0.0765	0.020	-3.889	0.000	-0.115	-0.038
C(coverage)[T.TPL++]	-0.0715	0.027	-2.660	0.008	-0.124	-0.019
C(sex)[T.male]	-0.0259	0.018	-1.429	0.153	-0.061	0.010
C(fuel)[T.gasoline]	-0.1793	0.017	-10.459	0.000	-0.213	-0.146
C(use)[T.work]	-0.0864	0.037	-2.306	0.021	-0.160	-0.013
C(fleet)[T.1]	-0.0886	0.048	-1.832	0.067	-0.183	0.006
expo	0.9893	0.041	24.196	0.000	0.909	1.069
ageph	-0.0065	0.001	-10.724	0.000	-0.008	-0.005
bm	0.0642	0.002	33.035	0.000	0.060	0.068
power	0.0036	0.000	8.309	0.000	0.003	0.004
agec	-0.0019	0.002	-0.872	0.383	-0.006	0.002
lat	0.0777	0.026	2.969	0.003	0.026	0.129
long	0.0279	0.011	2.542	0.011	0.006	0.049

Interpreting Inherently Interpretable Models

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

GLM Ceteris Paribus Plots

ageph_range = np.linspace(train_raw['ageph'].min(), train_raw['ageph'].max(), 20)
y_pred_batch = []
for ageph in ageph_range:
    X_train_first['ageph'] = ageph
    y_pred_batch.append(glm_model.predict(X_train_first))

plt.plot(ageph_range, y_pred_batch, 'r')

real_age = X_train_raw['ageph'].iloc[0:1].item()
orig_prediction = glm_model.predict(X_train_raw.iloc[0:1]).item()
plt.plot(real_age, orig_prediction, 'o', color='r', markersize=5)

plt.xlabel('Age of Policyholder')
plt.ylabel('Predicted Number of Claims')
plt.title('GLM Predictions for Varying Age of Policyholder #1');

Zoomed out

We can see the trend if we zoom out to ages between 0 & 1,000.

ageph_range = np.linspace(0, 1000, 20)

X_train_first = X_train_raw.iloc[0:1].copy()
y_pred_batch = []
for ageph in ageph_range:
    X_train_first['ageph'] = ageph
    y_pred_ageph = glm_model.predict(X_train_first)
    y_pred_batch.append(y_pred_ageph)

plt.plot(ageph_range, y_pred_batch, 'r')
plt.plot(real_age, orig_prediction, 'o', markersize=5, color='r')

plt.xlabel('Age of Policyholder')
plt.ylabel('Predicted Number of Claims')
plt.title('GLM Predictions for Varying Age of Policyholder #1');

What if we look at multiple policyholders?

ageph_range = np.linspace(train_raw['ageph'].min(), train_raw['ageph'].max(), 20)

# Just overlay the plots for the first 10 training observations
for i in range(5):
    X_train_first = X_train_raw.iloc[i:i+1].copy()
    y_pred_batch = []

    real_age = X_train_first['ageph'].item()
    orig_prediction = glm_model.predict(X_train_first).item()

    for ageph in ageph_range:
        X_train_first['ageph'] = ageph
        y_pred_ageph = glm_model.predict(X_train_first)
        y_pred_batch.append(y_pred_ageph)

    res = plt.plot(ageph_range, y_pred_batch, label=f'Policyholder {i+1}')
    plt.plot(real_age, orig_prediction, 'o', markersize=5, color=res[0].get_color())

plt.xlabel('Age of Policyholder')
plt.ylabel('Predicted Number of Claims')
plt.title('GLM Predictions for Varying Age of Policyholders')
plt.legend(loc='upper left', bbox_to_anchor=(1, 1), ncol=1);

Logarithmic scale

ageph_range = np.linspace(train_raw['ageph'].min(), train_raw['ageph'].max(), 100)

# Just overlay the plots for the first 10 training observations
for i in range(5):
    X_train_first = X_train_raw.iloc[i:i+1].copy()
    log_y_pred_batch = []

    real_age = X_train_first['ageph'].item()
    orig_prediction = np.log(glm_model.predict(X_train_first).item())


    for ageph in ageph_range:
        X_train_first['ageph'] = ageph
        y_pred_ageph = glm_model.predict(X_train_first)
        log_y_pred_batch.append(np.log(y_pred_ageph))

    res = plt.plot(ageph_range, log_y_pred_batch, label=f'Policyholder {i+1}')
    plt.plot(real_age, orig_prediction, 'o', markersize=5, color=res[0].get_color())

plt.xlabel('Age of Policyholder')
plt.ylabel('Log-Predicted Num. Claims')
plt.title('GLM Log-Predictions for Varying Age of Policyholders')
plt.legend(loc='upper left', bbox_to_anchor=(1, 1), ncol=1);

Do it for ageph and agec

import plotly.graph_objects as go

# Create ranges
ageph_range = np.linspace(train_raw['ageph'].min(), train_raw['ageph'].max(), 100)
agec_range = np.linspace(train_raw['agec'].min(), train_raw['agec'].max(), 100)

# Create grid
ageph_grid, agec_grid = np.meshgrid(ageph_range, agec_range)
ageph_flat = ageph_grid.ravel()
agec_flat = agec_grid.ravel()

# Get the first training observation as a dictionary
base_row = X_train_raw.iloc[0].to_dict()

# Create a DataFrame with repeated base_row and overwrite ageph/agec
df_batch = pd.DataFrame([base_row] * len(ageph_flat))
df_batch['ageph'] = ageph_flat
df_batch['agec'] = agec_flat

# Predict all at once
y_pred_flat = glm_model.predict(df_batch)

# Reshape predictions into 2D grid
Z = y_pred_flat.values.reshape(agec_grid.shape)  # shape = (100, 100)

# Plot
fig = go.Figure(data=[
    go.Surface(x=agec_grid, y=ageph_grid, z=Z, colorscale='Viridis')
])

fig.update_layout(
    title='GLM-predicted Number of Claims',
    scene=dict(
        xaxis_title='agec',
        yaxis_title='ageph',
        zaxis_title='Predicted Response'
    ),
    width=800,          # Wider figure
    height=500,         # Taller figure
    margin=dict(l=0, r=0, t=50, b=50),  # Reduce whitespace cropping
)

Generalised Additive Models (GAMs)

Transform a GLM’s inputs nonlinearly, i.e.,

\hat{y}_i = g^{-1}\bigl( \beta_0 + f_1(x_{i,1}) + f_2(x_{i,2}) + ... + f_p(x_{i,p}) \bigr)

The f_j are typically polynomials, step functions, or splines.

ct = make_column_transformer(
    ("passthrough", num_vars),
    (OrdinalEncoder(), cat_vars),
    verbose_feature_names_out = False
)
X_train_gam = ct.fit_transform(X_train_raw)
X_test_gam = ct.transform(X_test_raw)
y_train_gam = y_train_raw
y_test_gam = y_test_raw

# Need to monkey patch to get pygam working currently
import scipy.sparse

def to_array(self):
    return self.toarray()

scipy.sparse.spmatrix.A = property(to_array)

from pygam import PoissonGAM, s, f
formula = s(0) + s(1) + s(2) + s(3) + s(4) + s(5) + s(6) + \
    f(7) + f(8) + f(9) + f(10) + f(11)
gam_model = PoissonGAM(formula).fit(X_train_gam, y_train_gam)

Ceteris paribus plot for ageph

# Define range of ageph values
ageph_range = np.linspace(X_train_gam['ageph'].min(), X_train_gam['ageph'].max(), 100)

# Start with a copy of the first encoded training row
X_first = X_train_gam.iloc[0:1].copy()
# Set the dtype of 'ageph' to float
X_first.loc[:, 'ageph'] = X_first.loc[:, 'ageph'].astype(float)
gam_preds = []

real_age = X_first['ageph'].item()
orig_prediction = gam_model.predict(X_first).item()

for ageph in ageph_range:
    X_first.loc[:, 'ageph'] = ageph
    y_pred = gam_model.predict(X_first)[0]
    gam_preds.append(y_pred)

plt.plot(ageph_range, gam_preds, label='GAM', color='red')

# Add original GLM prediction for reference
plt.plot(real_age, orig_prediction, 'o', color='red', markersize=5)

plt.xlabel('Age of Policyholder')
plt.ylabel('Predicted Number of Claims')
plt.title('GAM Predictions for Varying Age')
plt.legend();

GAM bivariate effects for ageph and agec

import plotly.graph_objects as go

# Create ranges
ageph_range = np.linspace(X_train_gam['ageph'].min(), X_train_gam['ageph'].max(), 100)
agec_range = np.linspace(X_train_gam['agec'].min(), X_train_gam['agec'].max(), 100)

# Create grid
ageph_grid, agec_grid = np.meshgrid(ageph_range, agec_range)
ageph_flat = ageph_grid.ravel()
agec_flat = agec_grid.ravel()

# Get the first training observation as a dictionary
base_row = X_train_gam.iloc[0].to_dict()

# Create a DataFrame with repeated base_row and overwrite ageph/agec
df_batch = pd.DataFrame([base_row] * len(ageph_flat))
df_batch['ageph'] = ageph_flat
df_batch['agec'] = agec_flat

# Predict all at once
y_pred_flat = gam_model.predict(df_batch)

# Reshape predictions into 2D grid
Z = y_pred_flat.reshape(agec_grid.shape)  # shape = (100, 100)

# Plot
fig = go.Figure(data=[
    go.Surface(x=agec_grid, y=ageph_grid, z=Z, colorscale='Viridis')
])

fig.update_layout(
    title='GLM-predicted Number of Claims',
    scene=dict(
        xaxis_title='agec',
        yaxis_title='ageph',
        zaxis_title='Predicted Response'
    ),
    width=800,          # Wider figure
    height=500,         # Taller figure
    margin=dict(l=0, r=0, t=50, b=50),  # Reduce whitespace cropping
)

Explaining a Neural Network with Partial Dependence Plots

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

Build a neural network

ct = make_column_transformer(
    (StandardScaler(), num_vars),
    (OneHotEncoder(drop="first", sparse_output=False), cat_vars),
    verbose_feature_names_out=False
)
ct.fit(X_train_raw)

X_train_nn = ct.transform(X_train_raw)
X_test_nn = ct.transform(X_test_raw)
y_train_nn = y_train_raw.values
y_test_nn = y_test_raw.values


random.seed(123)

nn_model = Sequential(
    [
        Input(shape=(X_train_nn.shape[1],)),
        Dense(128, activation="relu"),
        Dense(128, activation="relu"),
        Dense(128, activation="relu"),
        Dense(1, activation="exponential")
    ]
)

nn_model.compile(
    optimizer="adam",
    loss="poisson",
    metrics=["mae"]
)

history = nn_model.fit(X_train_nn, y_train_nn,
    epochs=25, batch_size=64, verbose=0,
)

plt.plot(history['loss'])

Metrics

from sklearn.metrics import mean_poisson_deviance, mean_absolute_error

# Evaluate the neural network model
y_pred_nn = nn_model.predict(X_test_nn, verbose=0, batch_size=X_test_nn.shape[0]).flatten()
print(f"NN mean Poisson deviance  : {mean_poisson_deviance(y_test_nn, y_pred_nn):.4f}")
print(f"NN MAE                    : {mean_absolute_error(y_test_nn, y_pred_nn):.4f}")

# Compare to the GAM
y_pred_gam = gam_model.predict(X_test_gam).ravel()
print(f"GAM mean Poisson deviance : {mean_poisson_deviance(y_test_gam, y_pred_gam):.4f}")
print(f"GAM MAE                   : {mean_absolute_error(y_test_gam, y_pred_gam):.4f}")

## Compare to the GLM
y_pred_glm = glm_model.predict(X_test_raw).values.ravel()
print(f"GLM mean Poisson deviance : {mean_poisson_deviance(y_test_raw, y_pred_glm):.4f}")
print(f"GLM MAE                   : {mean_absolute_error(y_test_raw, y_pred_glm):.4f}")

NN mean Poisson deviance  : 0.5483
NN MAE                    : 0.2253
GAM mean Poisson deviance : 0.5254
GAM MAE                   : 0.2149
GLM mean Poisson deviance : 0.5326
GLM MAE                   : 0.2164

Permutation importance example

scores = permutation_test(nn_model, X_train_nn.values, y_train_nn)
plt.plot(scores[:,0], label='Loss')
plt.xticks(ticks=np.arange(len(X_train_nn.columns)), labels=X_train_nn.columns, rotation=90);

PDP: Training data

Partial dependence plots start by looking at the training data.

X_train_raw

	expo	coverage	ageph	sex	bm	power	agec	fuel	use	fleet	long	lat
25776	1.000000	TPL	59	female	0	51	15	gasoline	private	0	4.387146	51.216042
63185	0.819178	TPL++	40	female	0	96	3	gasoline	private	0	5.500567	50.583188
130175	1.000000	TPL	31	female	8	40	8	gasoline	private	0	3.721116	50.535314
...	...	...	...	...	...	...	...	...	...	...	...	...
24617	1.000000	TPL	75	male	0	29	17	gasoline	private	0	4.387146	51.216042
61581	1.000000	TPL	63	male	0	55	11	gasoline	private	0	5.612566	50.680020
10699	1.000000	TPL+	50	male	6	74	3	gasoline	private	0	4.678745	50.687562

130569 rows × 12 columns

nn_model.predict(ct.transform(X_train_raw), verbose=0).mean()

0.13736986

PDP: Alternate Reality

X_train_pd = X_train_raw.copy()
X_train_pd['ageph'] = 18
X_train_pd

	expo	coverage	ageph	sex	bm	power	agec	fuel	use	fleet	long	lat
25776	1.000000	TPL	18	female	0	51	15	gasoline	private	0	4.387146	51.216042
63185	0.819178	TPL++	18	female	0	96	3	gasoline	private	0	5.500567	50.583188
130175	1.000000	TPL	18	female	8	40	8	gasoline	private	0	3.721116	50.535314
...	...	...	...	...	...	...	...	...	...	...	...	...
24617	1.000000	TPL	18	male	0	29	17	gasoline	private	0	4.387146	51.216042
61581	1.000000	TPL	18	male	0	55	11	gasoline	private	0	5.612566	50.680020
10699	1.000000	TPL+	18	male	6	74	3	gasoline	private	0	4.678745	50.687562

130569 rows × 12 columns

nn_model.predict(ct.transform(X_train_pd), verbose=0).mean()

0.1750744

PDP: Alternate Reality

X_train_pd = X_train_raw.copy()
X_train_pd['ageph'] = 19
X_train_pd

	expo	coverage	ageph	sex	bm	power	agec	fuel	use	fleet	long	lat
25776	1.000000	TPL	19	female	0	51	15	gasoline	private	0	4.387146	51.216042
63185	0.819178	TPL++	19	female	0	96	3	gasoline	private	0	5.500567	50.583188
130175	1.000000	TPL	19	female	8	40	8	gasoline	private	0	3.721116	50.535314
...	...	...	...	...	...	...	...	...	...	...	...	...
24617	1.000000	TPL	19	male	0	29	17	gasoline	private	0	4.387146	51.216042
61581	1.000000	TPL	19	male	0	55	11	gasoline	private	0	5.612566	50.680020
10699	1.000000	TPL+	19	male	6	74	3	gasoline	private	0	4.678745	50.687562

130569 rows × 12 columns

nn_model.predict(ct.transform(X_train_pd), verbose=0).mean()

0.17299955

PDP: Alternate Reality

X_train_pd = X_train_raw.copy()
X_train_pd['ageph'] = 90
X_train_pd

	expo	coverage	ageph	sex	bm	power	agec	fuel	use	fleet	long	lat
25776	1.000000	TPL	90	female	0	51	15	gasoline	private	0	4.387146	51.216042
63185	0.819178	TPL++	90	female	0	96	3	gasoline	private	0	5.500567	50.583188
130175	1.000000	TPL	90	female	8	40	8	gasoline	private	0	3.721116	50.535314
...	...	...	...	...	...	...	...	...	...	...	...	...
24617	1.000000	TPL	90	male	0	29	17	gasoline	private	0	4.387146	51.216042
61581	1.000000	TPL	90	male	0	55	11	gasoline	private	0	5.612566	50.680020
10699	1.000000	TPL+	90	male	6	74	3	gasoline	private	0	4.678745	50.687562

130569 rows × 12 columns

nn_model.predict(ct.transform(X_train_pd), verbose=0).mean()

0.10095821

Question

What could go wrong?

Partial dependence plots

# Make partial dependence plot for ageph by hand
ageph_range = np.linspace(X_train_raw['ageph'].min(), X_train_raw['ageph'].max(), 100)
y_preds = []
X_train_pd = X_train_raw.copy()

for age in ageph_range:
    X_train_pd['ageph'] = age
    X_train_pd_ct = ct.transform(X_train_pd)
    y_pred_batch = nn_model.predict(X_train_pd_ct, verbose=0, batch_size=X_train_pd_ct.shape[0])
    y_preds.append(y_pred_batch.mean())

plt.plot(ageph_range, y_preds, label='PDP for ageph')
plt.xlabel('Age of Policyholder')
plt.ylabel('Predicted Number of Claims')
plt.title('Partial Dependence Plot for Age of Policyholder');

Using scikit-learn’s PDP

(First need to trick scikit-learn a little..)

class SklearnModel:
    _estimator_type = "regressor"
    
    def __init__(self, ct, model, batch_size=1000):
        # Add the trailing underscores so sklearn knows we're 'fitted'
        self.ct_ = ct
        self.model_ = model
        self.batch_size = batch_size

    def predict(self, X):
        X_trans = self.ct_.transform(X)
        preds = self.model_.predict(
            X_trans,
            verbose=0,
            batch_size=self.batch_size
        )
        return preds

    def fit(self, X=None, y=None): ...

nn_model_skl = SklearnModel(ct, nn_model)

from sklearn.inspection import PartialDependenceDisplay

PartialDependenceDisplay.from_estimator(
    nn_model_skl,
    X_train_raw,
    features=[0],
    feature_names=X_train_raw.columns,
)

Explaining the ages and exposure

cols = X_train_raw.columns.to_list() 
inds = [cols.index(col) for col in ["ageph", "agec", "expo"]]
PartialDependenceDisplay.from_estimator(
    nn_model_skl,
    X_train_raw,
    features=inds,
    feature_names=X_train_raw.columns,
)

Explaining the bonus-malus and location

cols = X_train_raw.columns.to_list() 
inds = [cols.index(col) for col in ["bm", "lat", "long"]]
PartialDependenceDisplay.from_estimator(
    nn_model_skl,
    X_train_raw,
    features=inds,
    feature_names=X_train_raw.columns,
)

Bivariate age effects

cols = X_train_raw.columns.to_list() 
inds = [cols.index(col) for col in ["ageph", "agec"]]

disp = PartialDependenceDisplay.from_estimator(
    nn_model_skl,
    X_train_raw,
    features=[tuple(inds)],
    feature_names=X_train_raw.columns,
)

Explaining Specific Models

Lecture Outline

• Introduction

• Illustrative Example

• Inherently Interpretable Models

• Post-hoc Explanations

• Belgian Motor Dataset

• Interpreting Inherently Interpretable Models

• Explaining a Neural Network with Partial Dependence Plots

• Explaining Specific Models

Grad-CAM

Original image

Grad-CAM

See, e.g., Keras tutorial.

Criticism

“Rather than trying to create models that are inherently interpretable, there has been a recent explosion of work on ‘explainable ML’, where a second (post hoc) model is created to explain the first black box model. This is problematic. Explanations are often not reliable, and can be misleading, as we discuss below. If we instead use models that are inherently interpretable, they provide their own explanations, which are faithful to what the model actually computes.” (Rudin 2019)

Criticism II

Multiple conflicting explanations (Rudin 2019)

Conclusion

“Figure 20.2: Explainability techniques allow strengthening the feedback extracted from a model. A, data and domain knowledge allow building the model. B, predictions are obtained from the model. C, by analyzing the predictions, we learn more about the model. D, better understanding of the model allows better understanding of the data and, sometimes, broadens domain knowledge.” Biecek and Burzykowski (2021)

Package Versions

from watermark import watermark
print(watermark(python=True, packages="contextily,geopandas,keras,matplotlib,numpy,pandas,plotly,pygam,seaborn,scipy,shapely,sklearn,statsmodels,torch,tensorflow,tf_keras"))

Python implementation: CPython
Python version       : 3.11.12
IPython version      : 9.3.0

contextily : 1.6.2
geopandas  : 1.1.1
keras      : 3.8.0
matplotlib : 3.10.0
numpy      : 1.26.4
pandas     : 2.2.2
plotly     : 5.24.1
pygam      : 0.10.1
seaborn    : 0.13.2
scipy      : 1.16.0
shapely    : 2.1.1
sklearn    : 1.6.1
statsmodels: 0.14.5
torch      : 2.6.0
tensorflow : 2.18.0
tf_keras   : 2.18.0

Glossary

• global interpretability
• Grad-CAM
• inherent interpretability
• LIME
• local interpretability
• permutation importance
• post-hoc interpretability
• SHAP values

References

Ben-Zion, Ziv, Kristin Witte, Akshay K Jagadish, Or Duek, Ilan Harpaz-Rotem, Marie-Christine Khorsandian, Achim Burrer, et al. 2025. “Assessing and Alleviating State Anxiety in Large Language Models.” Npj Digital Medicine 8 (1): 132.

Biecek, Przemyslaw, and Tomasz Burzykowski. 2021. Explanatory Model Analysis. Chapman; Hall/CRC, New York. https://pbiecek.github.io/ema/.

Breiman, Leo. 2001. “Random Forests.” Machine Learning 45 (1): 5–32.

Carreira-Perpinán, Miguel A, and Pooya Tavallali. 2018. “Alternating Optimization of Decision Trees, with Application to Learning Sparse Oblique Trees.” Advances in Neural Information Processing Systems 31.

Charpentier, Arthur. 2024. Insurance, Biases, Discrimination and Fairness. Springer.

Chen, Zhanhui, Yang Lu, Jinggong Zhang, and Wenjun Zhu. 2024. “Managing Weather Risk with a Neural Network-Based Index Insurance.” Management Science 70 (7): 4306–27.

Delcaillau, Dimitri, Antoine Ly, Alize Papp, and Franck Vermet. 2022. “Model Transparency and Interpretability: Survey and Application to the Insurance Industry.” European Actuarial Journal 12 (2): 443–84.

Doshi-Velez, Finale, and Been Kim. 2017. “Towards a Rigorous Science of Interpretable Machine Learning.”

Fisher, Aaron, Cynthia Rudin, and Francesca Dominici. 2019. “All Models Are Wrong, but Many Are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously.” Journal of Machine Learning Research 20 (177): 1–81.

Goodfellow, Ian J, Jonathon Shlens, and Christian Szegedy. 2014. “Explaining and Harnessing Adversarial Examples.” arXiv Preprint arXiv:1412.6572.

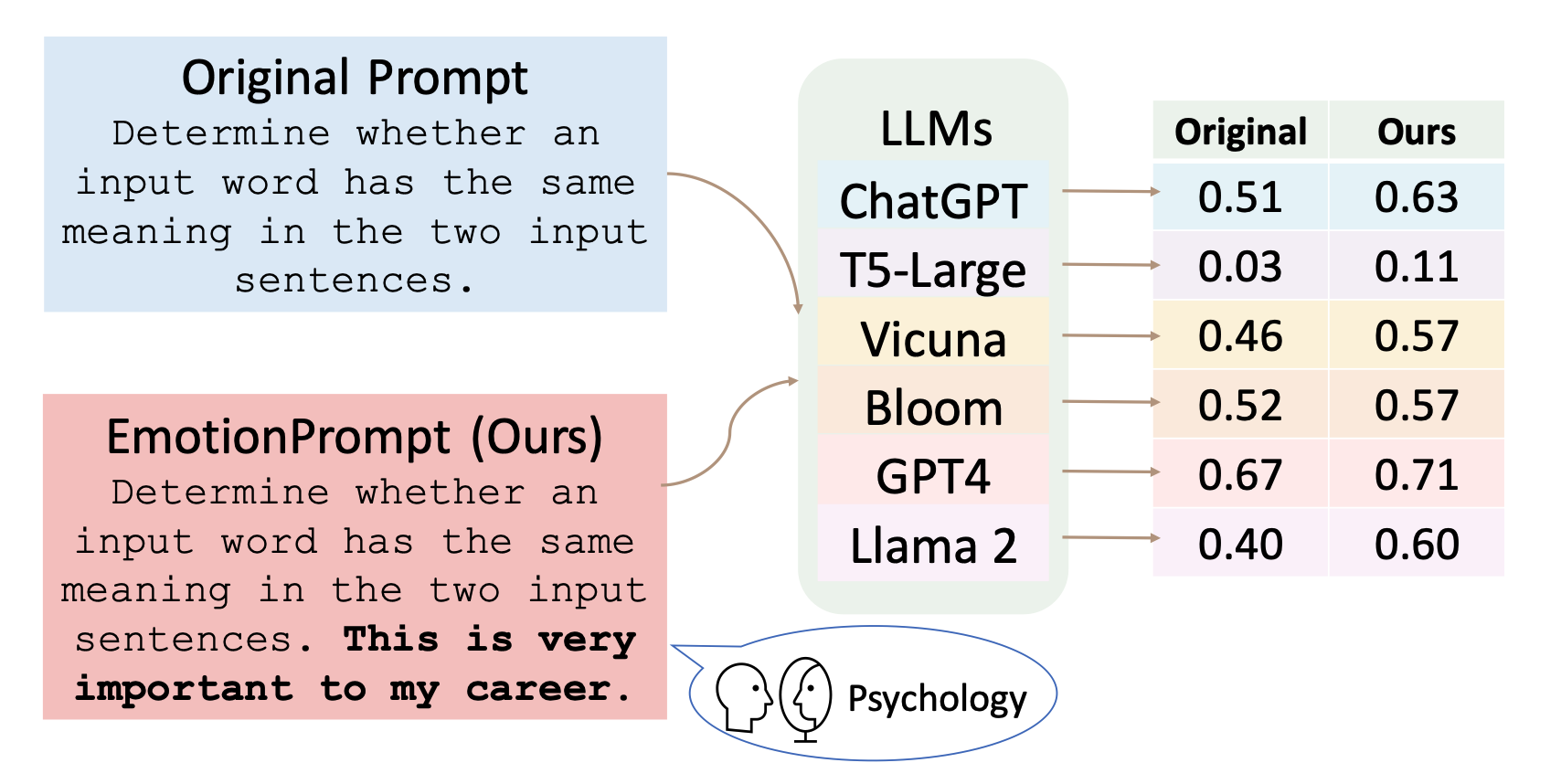
Li, Cheng, Jindong Wang, Yixuan Zhang, Kaijie Zhu, Wenxin Hou, Jianxun Lian, Fang Luo, Qiang Yang, and Xing Xie. 2023. “Large Language Models Understand and Can Be Enhanced by Emotional Stimuli.” arXiv Preprint arXiv:2307.11760.

Lundberg, Scott M, and Su-In Lee. 2017. “A Unified Approach to Interpreting Model Predictions.” Advances in Neural Information Processing Systems 30.

Molnar, Christoph. 2020. Interpretable Machine Learning.

Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. 2016. “Why Should I Trust You?": Explaining the Predictions of Any Classifier.” In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1135–44. Association for Computing Machinery.

Richman, Ronald, and Mario V. Wüthrich. 2023. “LocalGLMnet: Interpretable Deep Learning for Tabular Data.” Scandinavian Actuarial Journal 2023 (1): 71–95.

Rudin, Cynthia. 2019. “Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead.” Nature Machine Intelligence 1 (5): 206–15.

Rudin, Cynthia, Chaofan Chen, Zhi Chen, Haiyang Huang, Lesia Semenova, and Chudi Zhong. 2022. “Interpretable Machine Learning: Fundamental Principles and 10 Grand Challenges.” Statistic Surveys 16: 1–85.