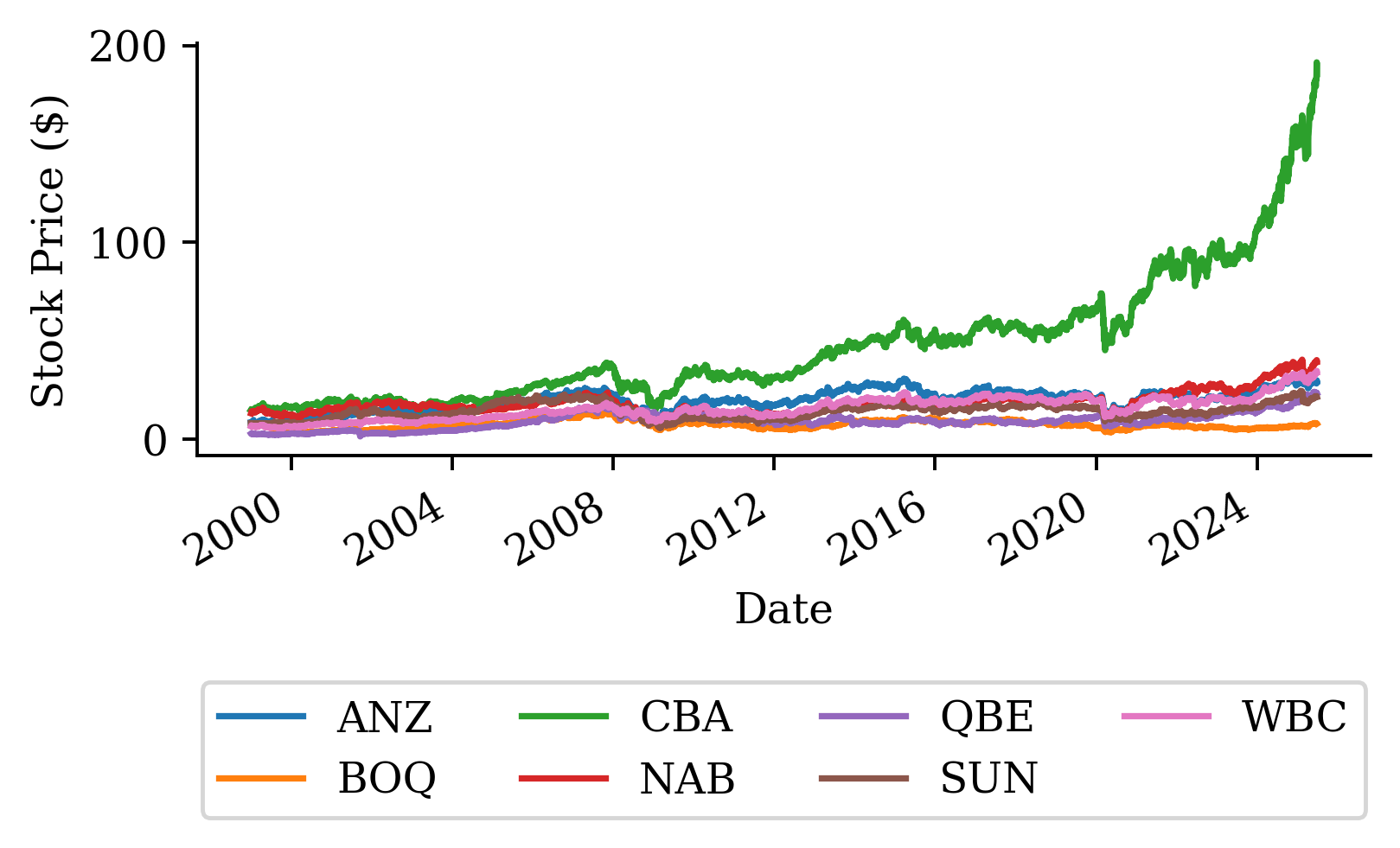
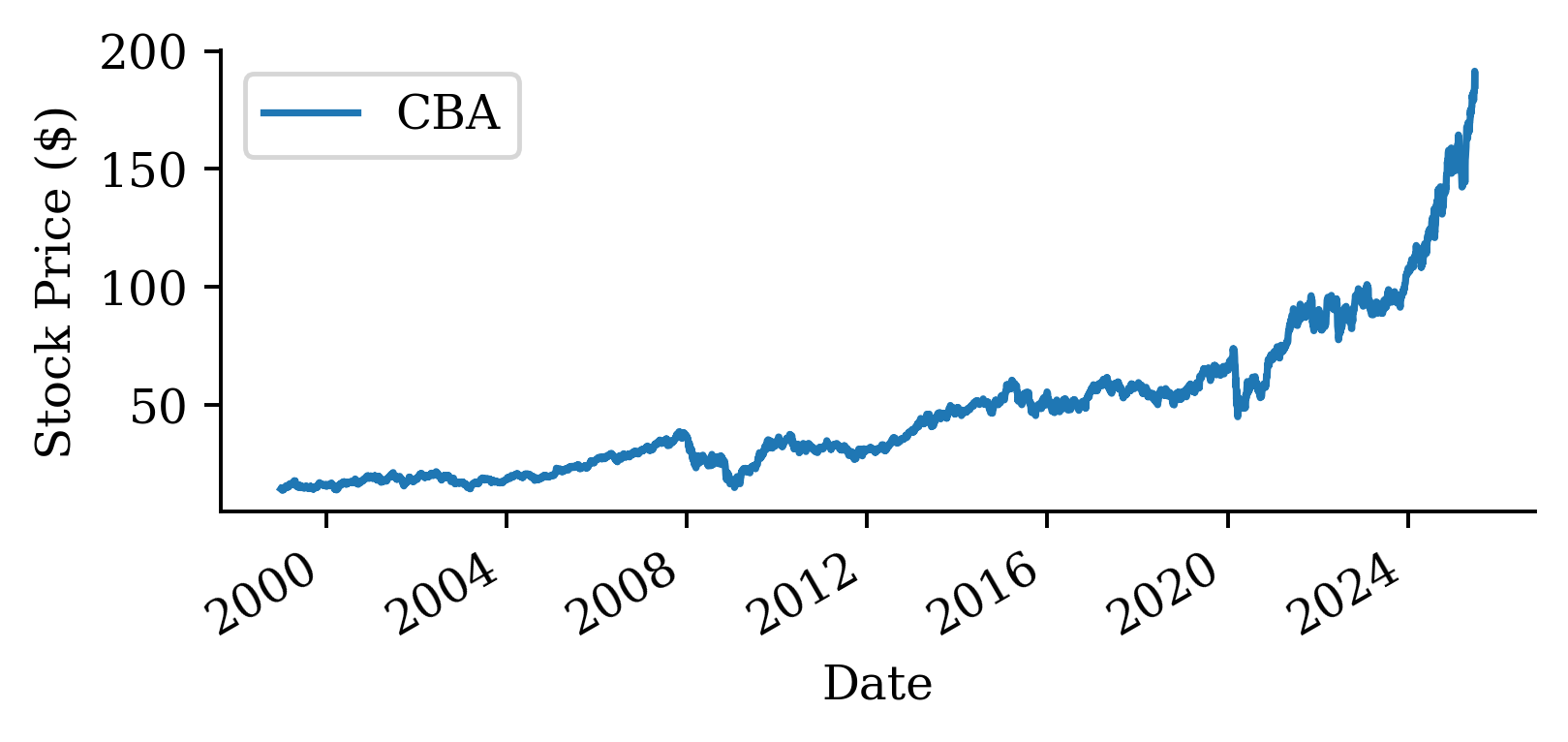
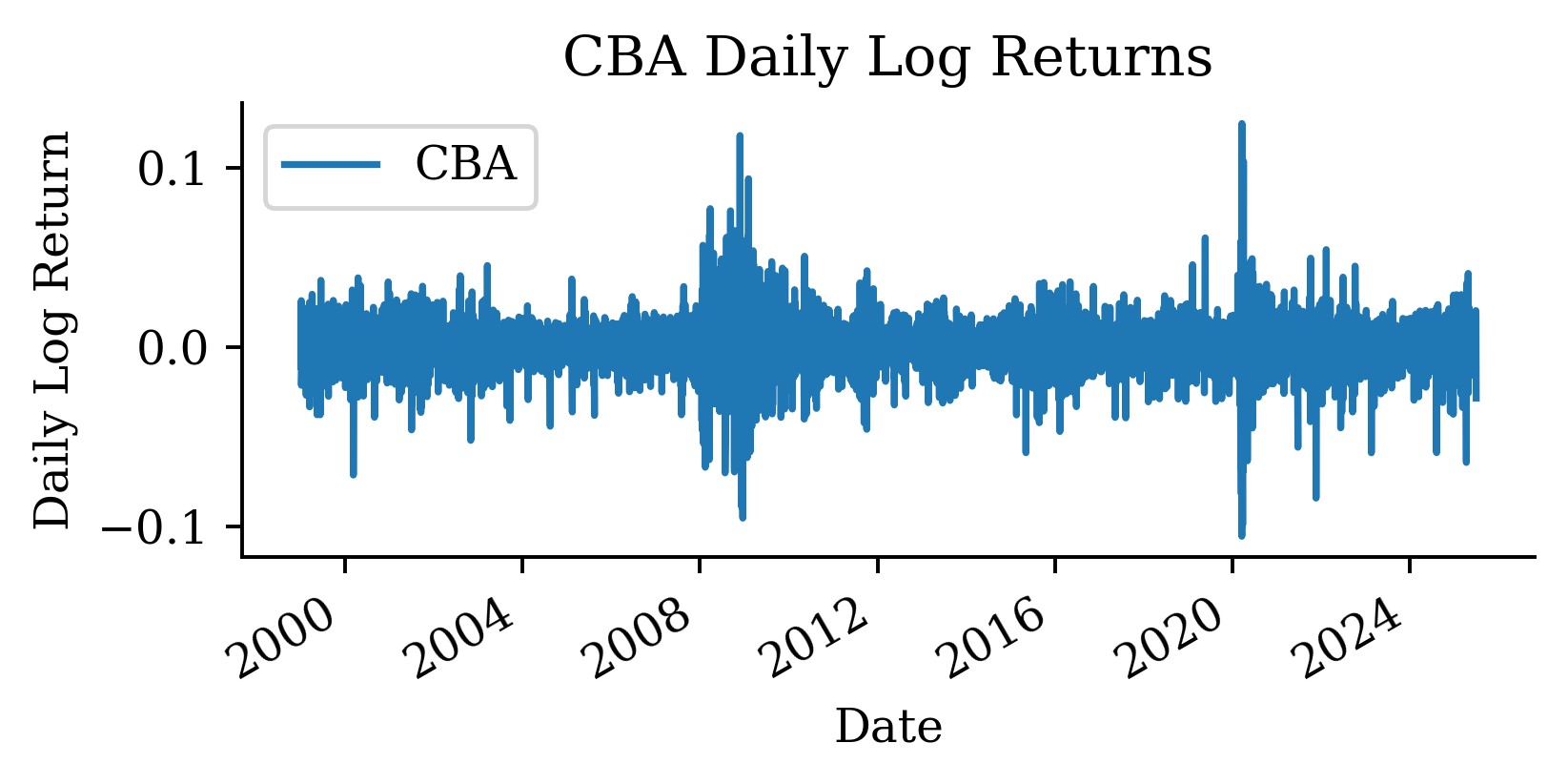
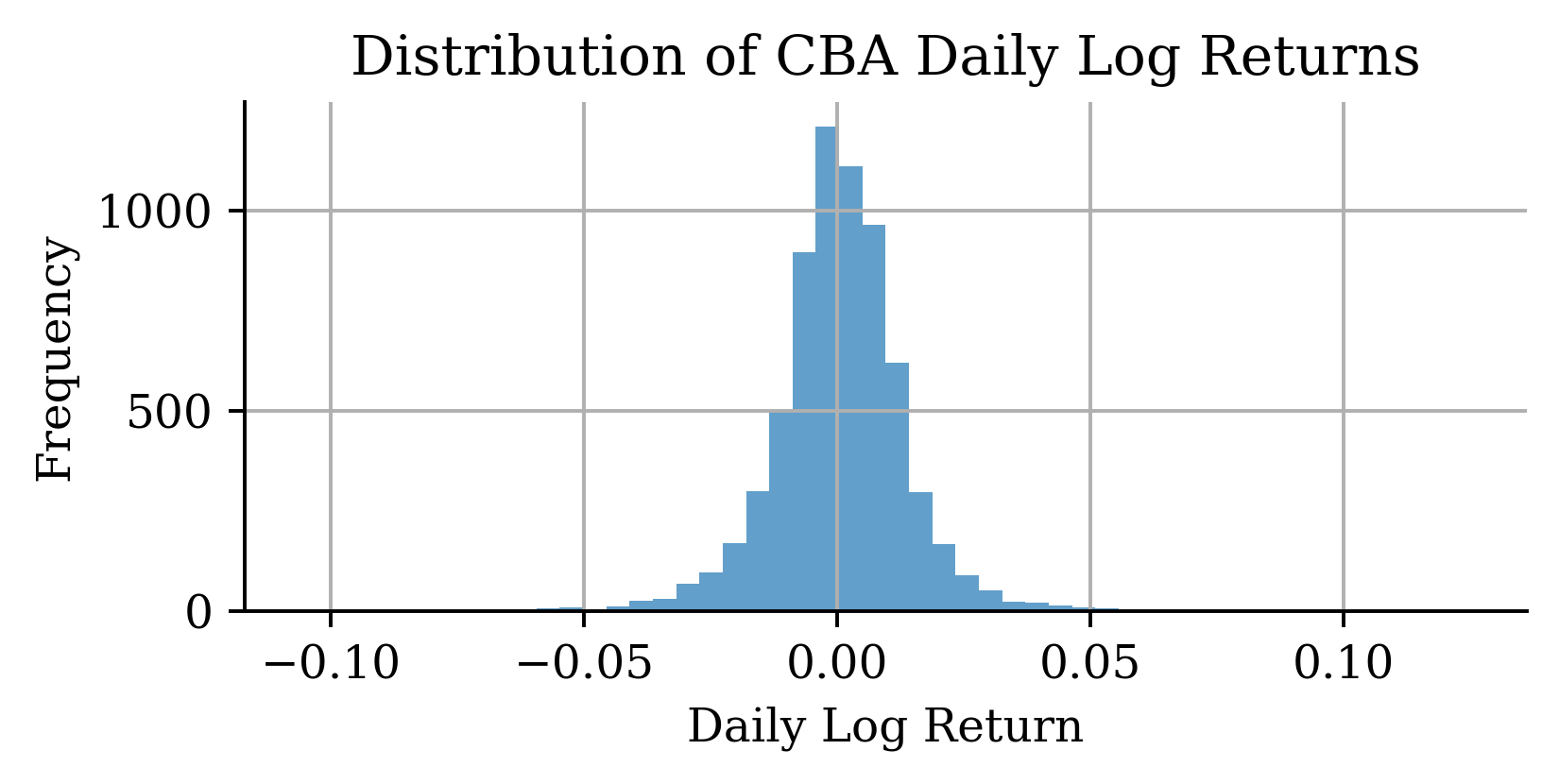
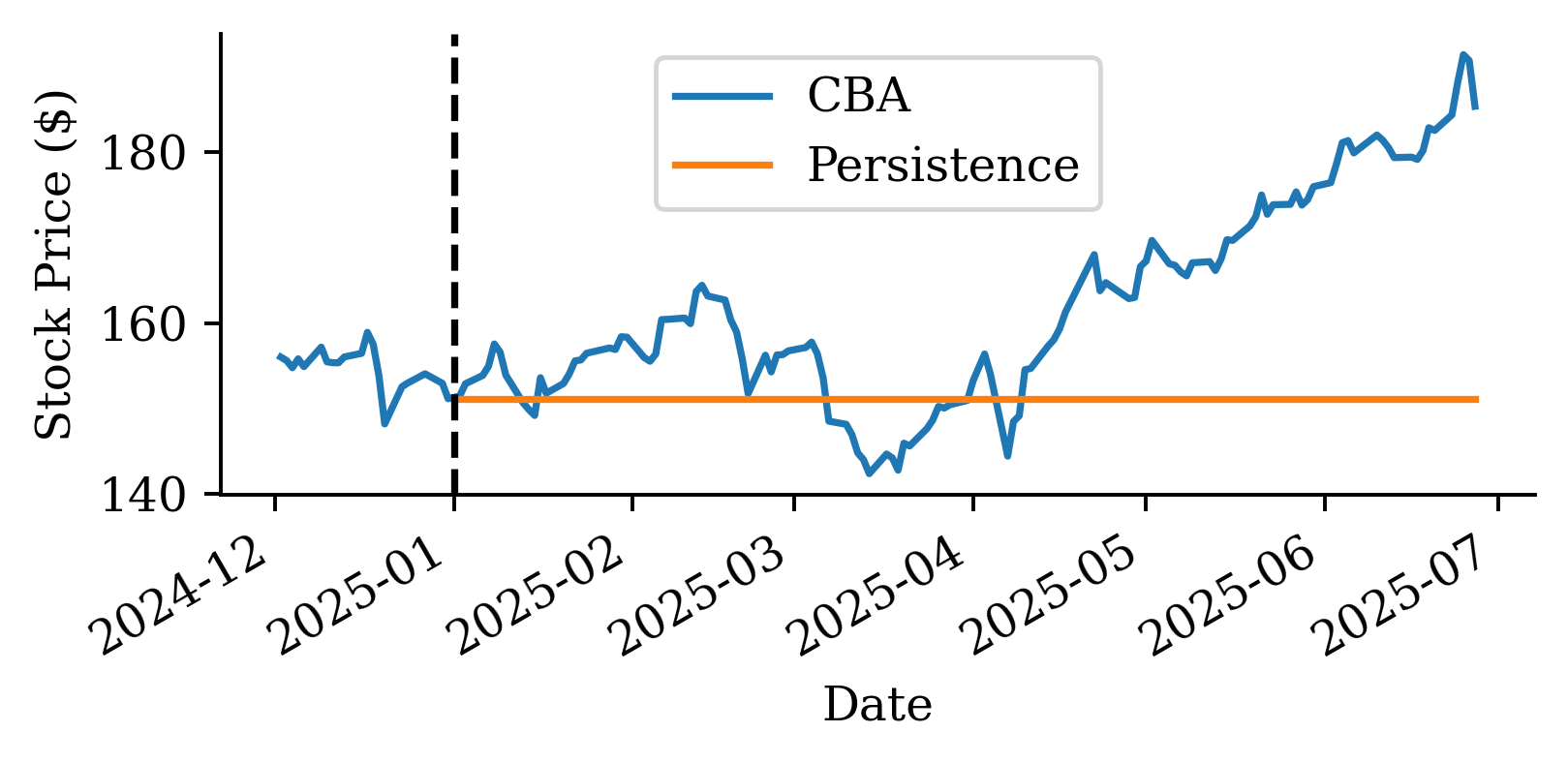
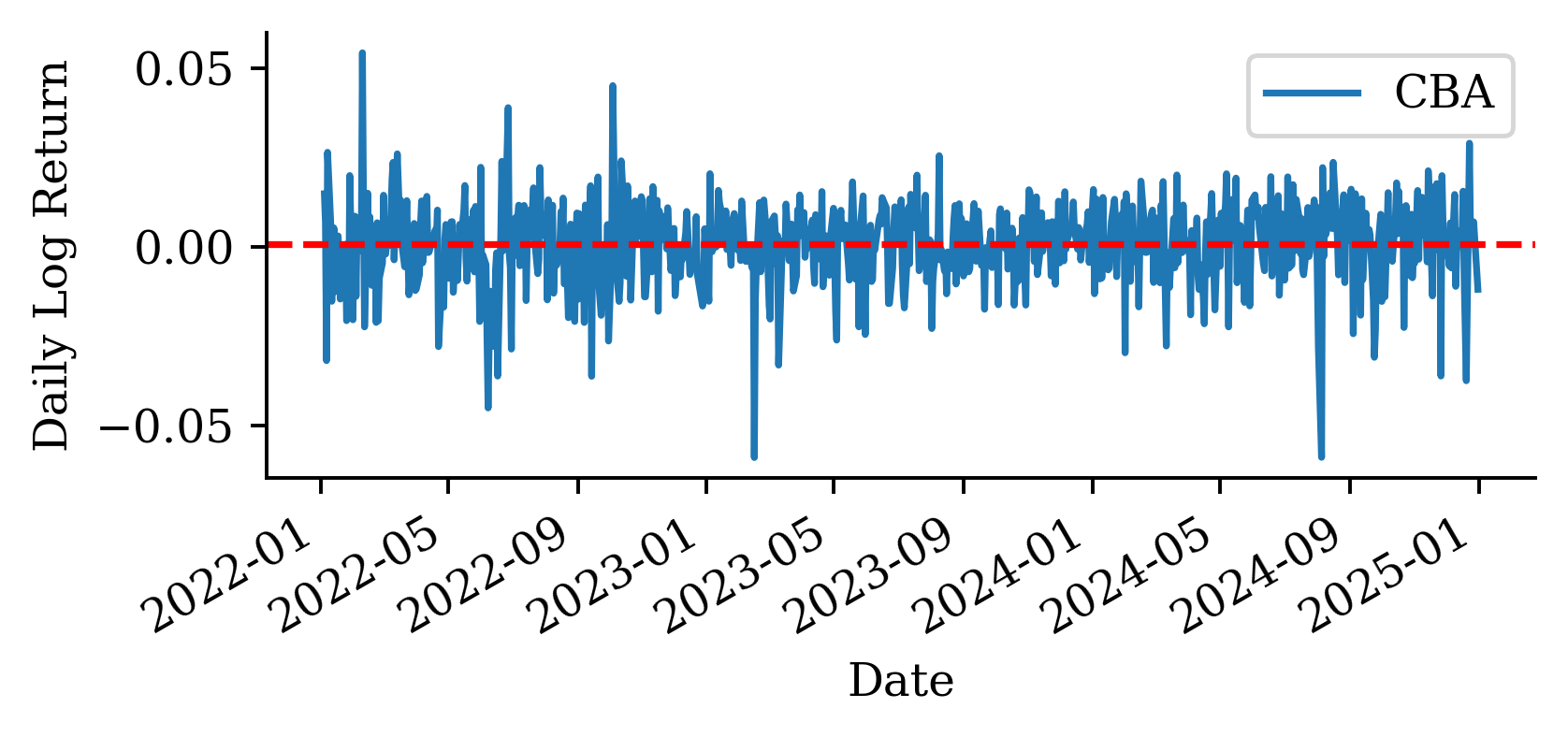
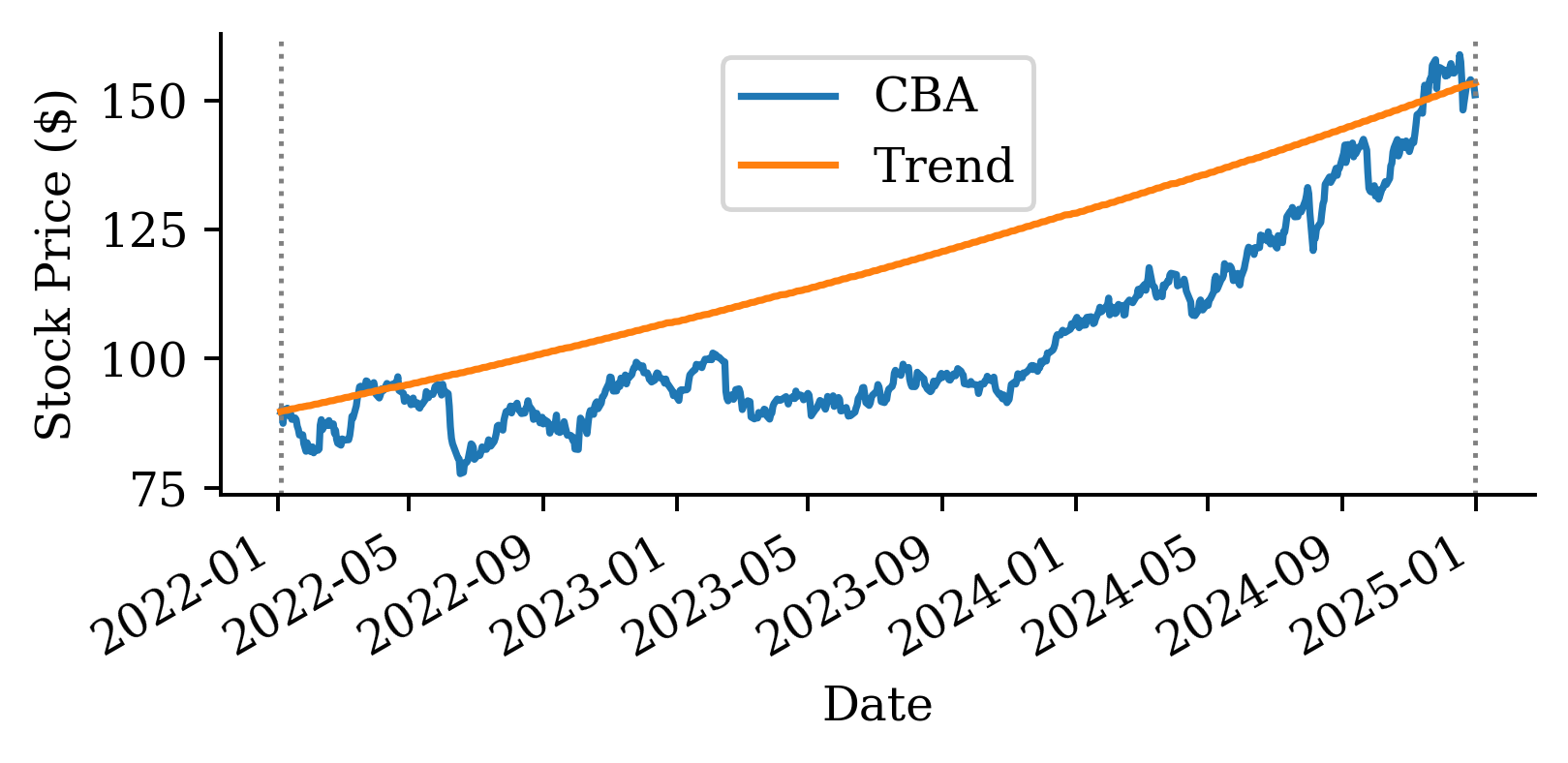
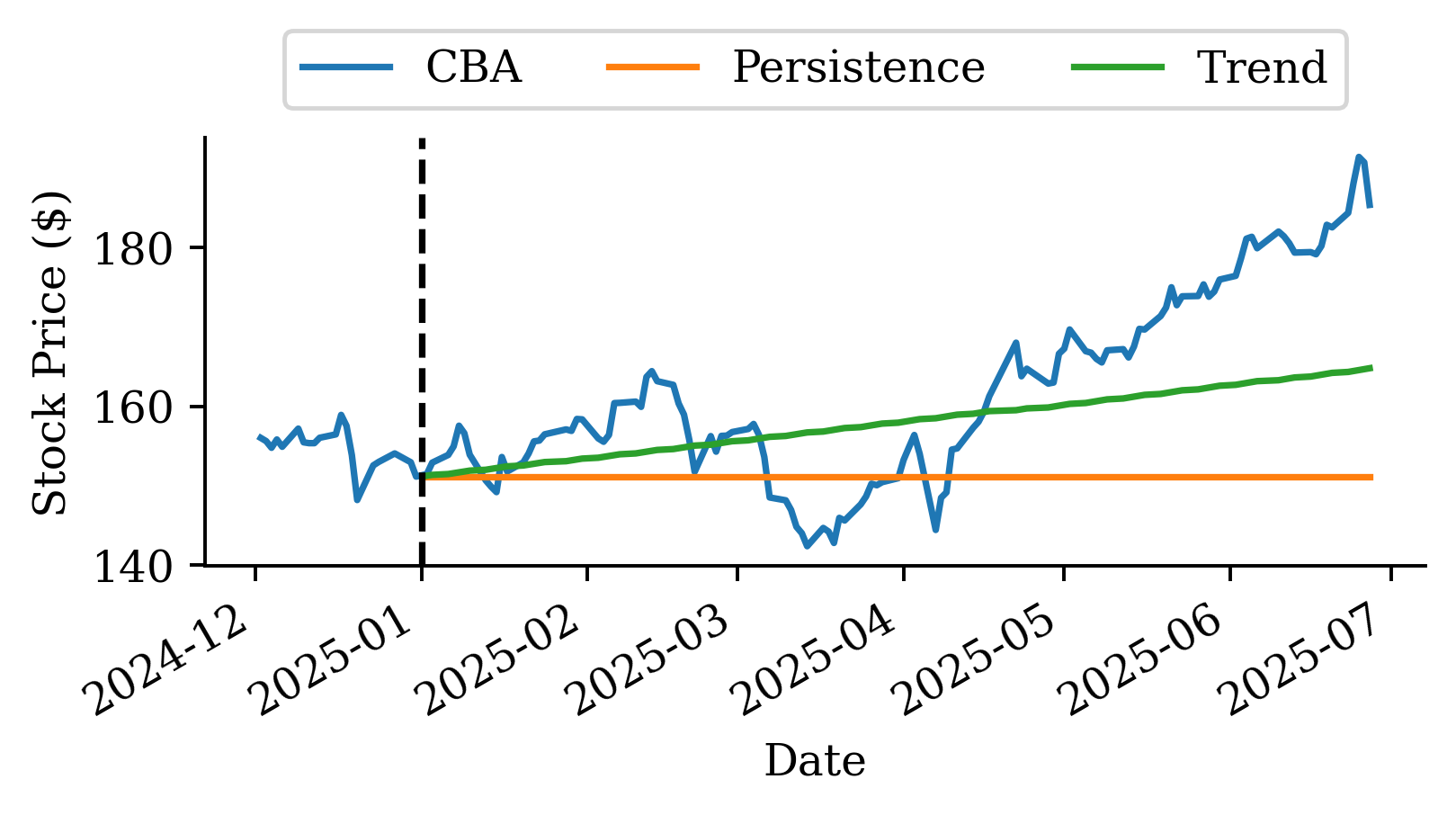
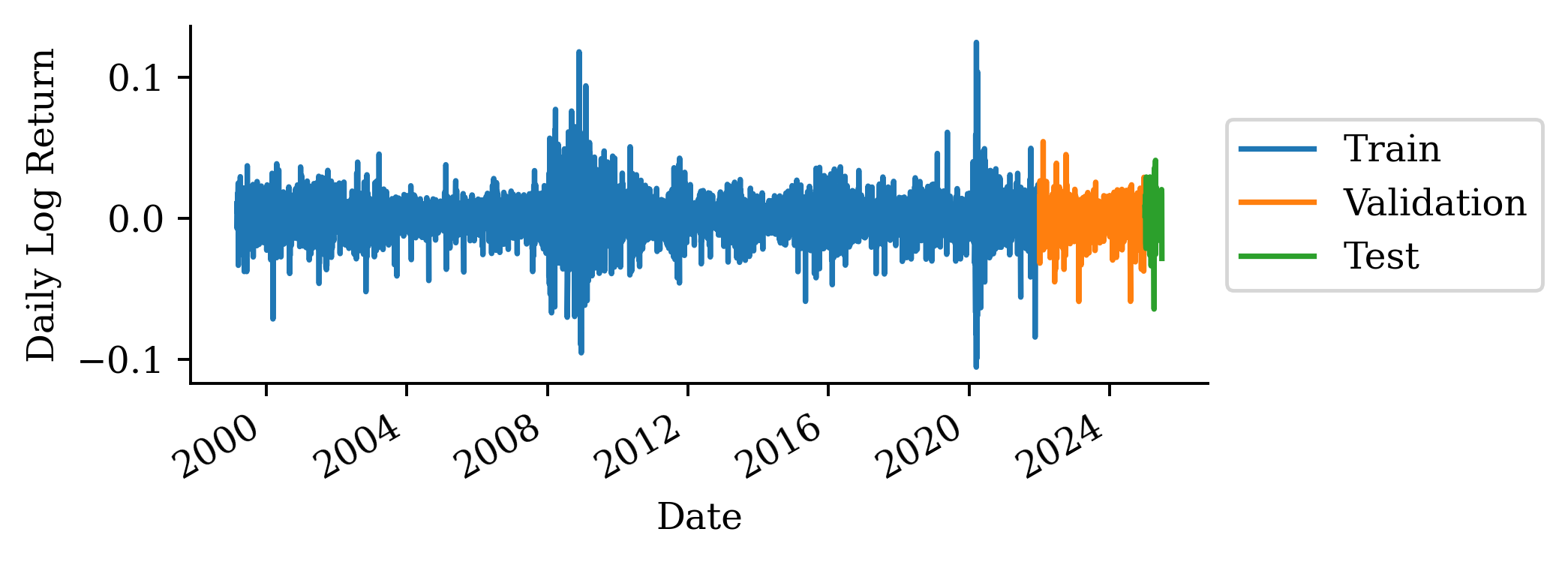
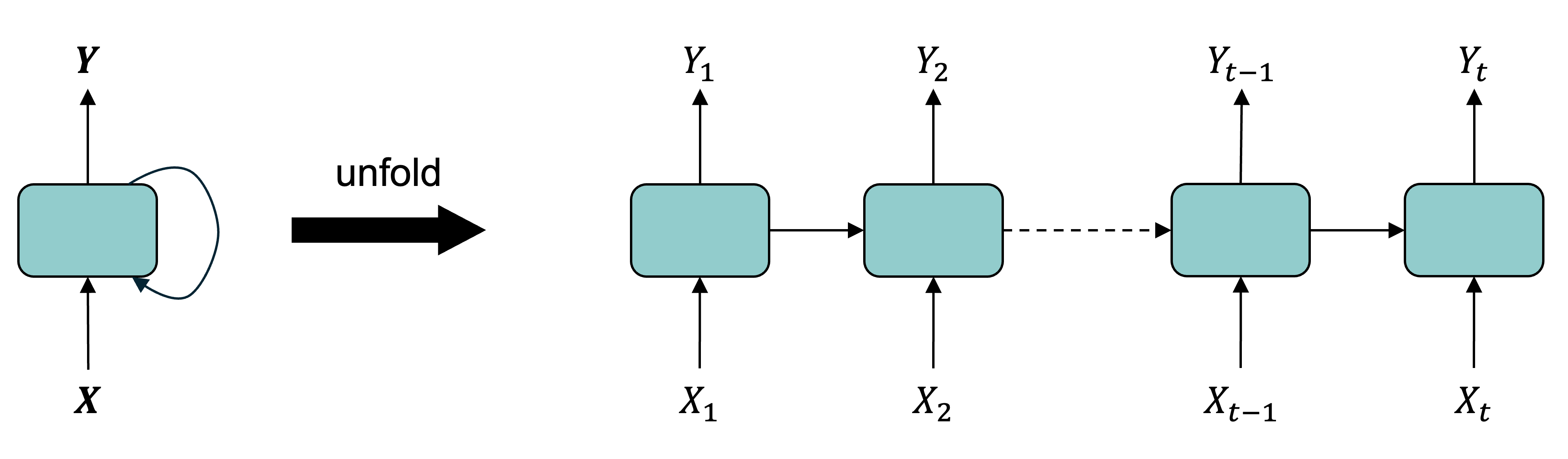
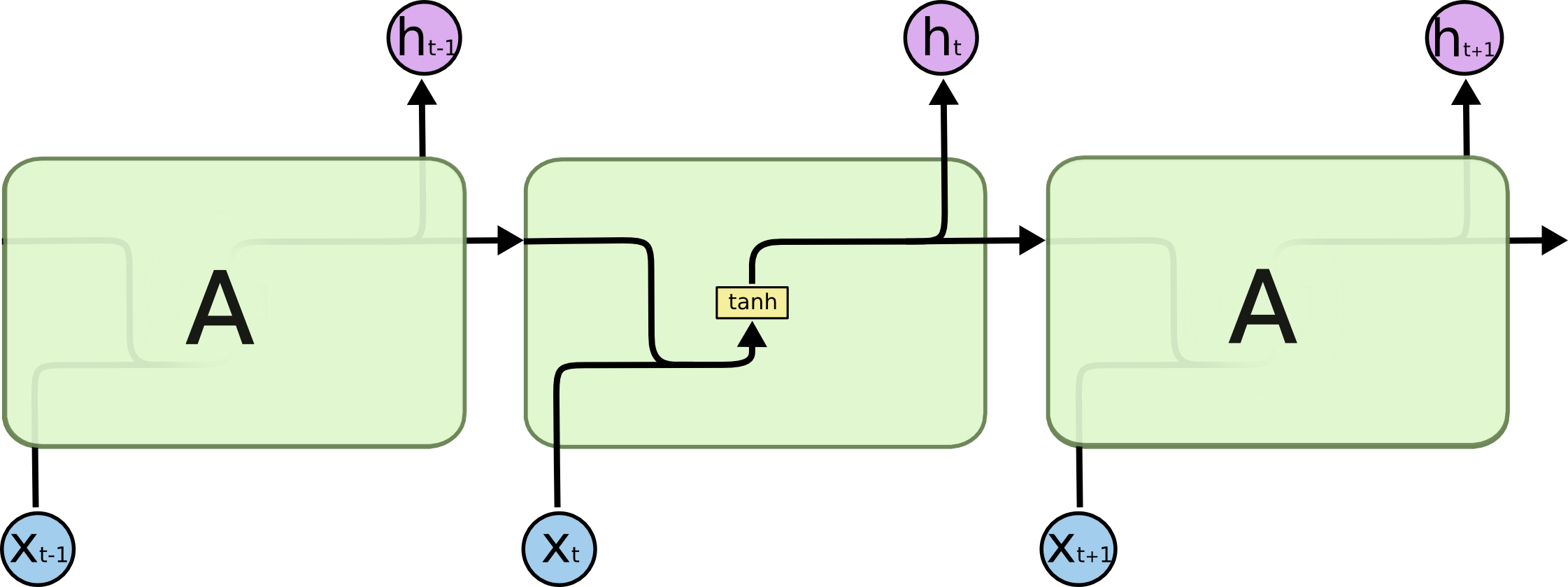
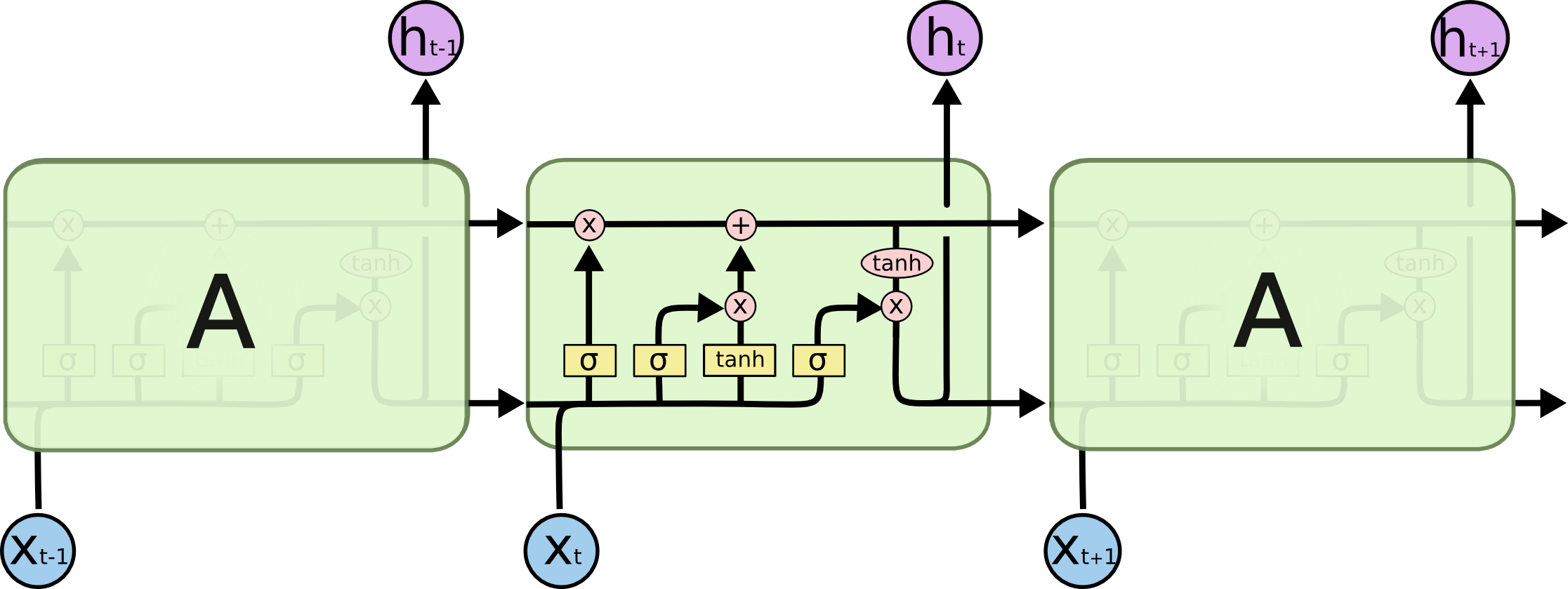
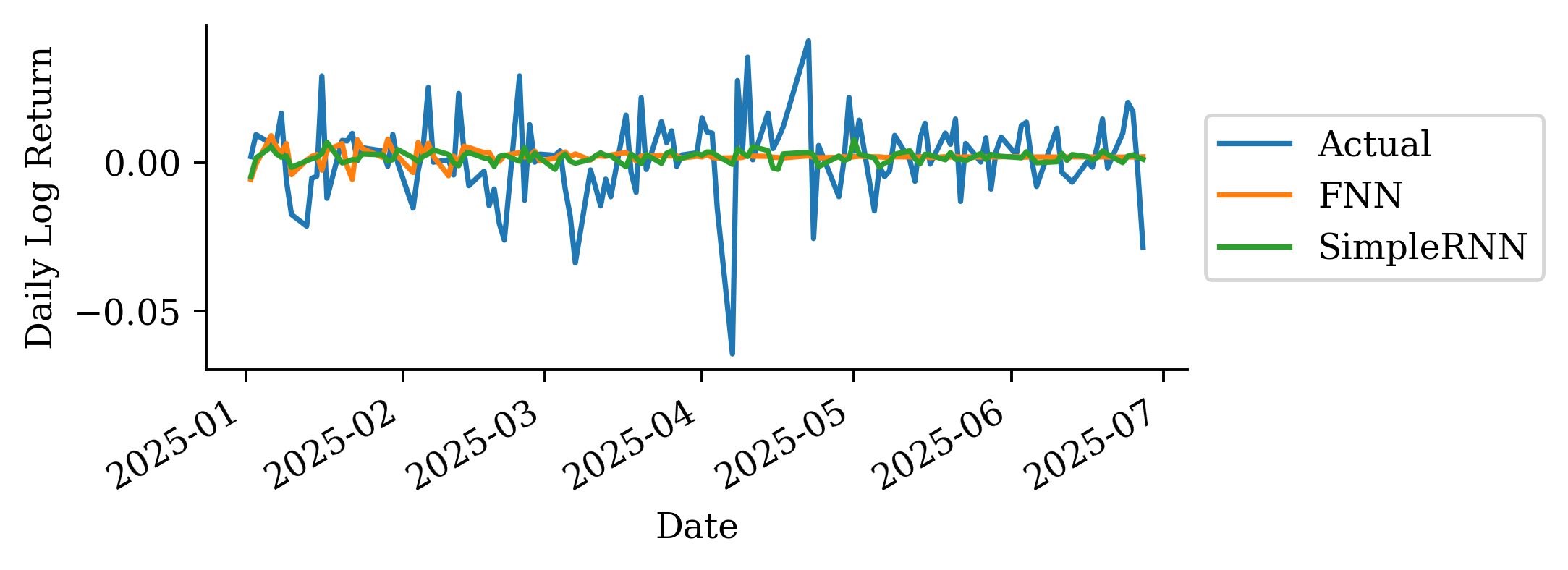
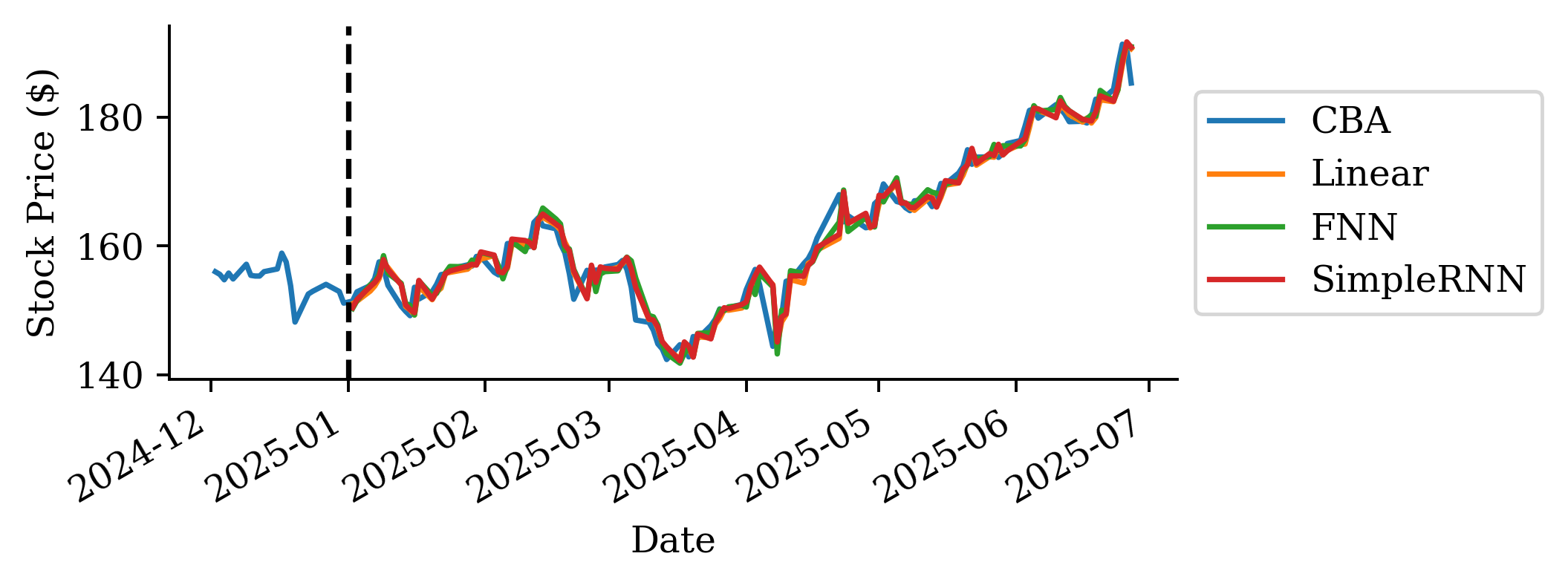
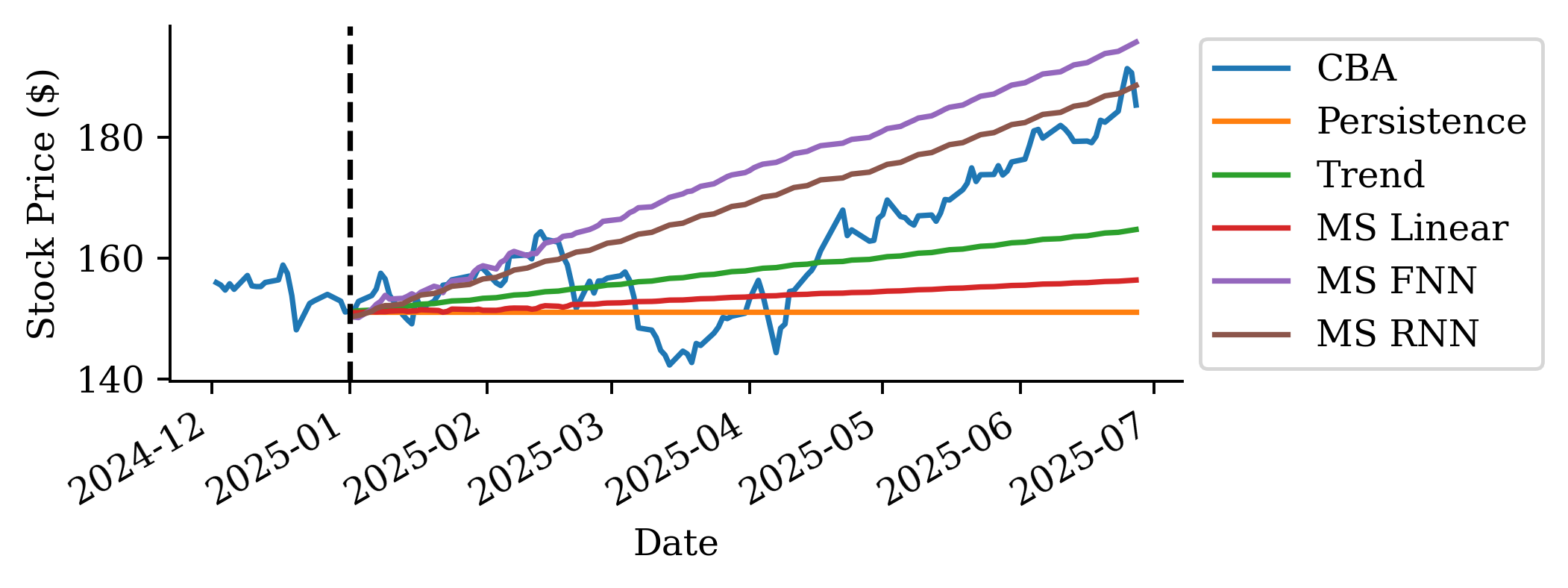
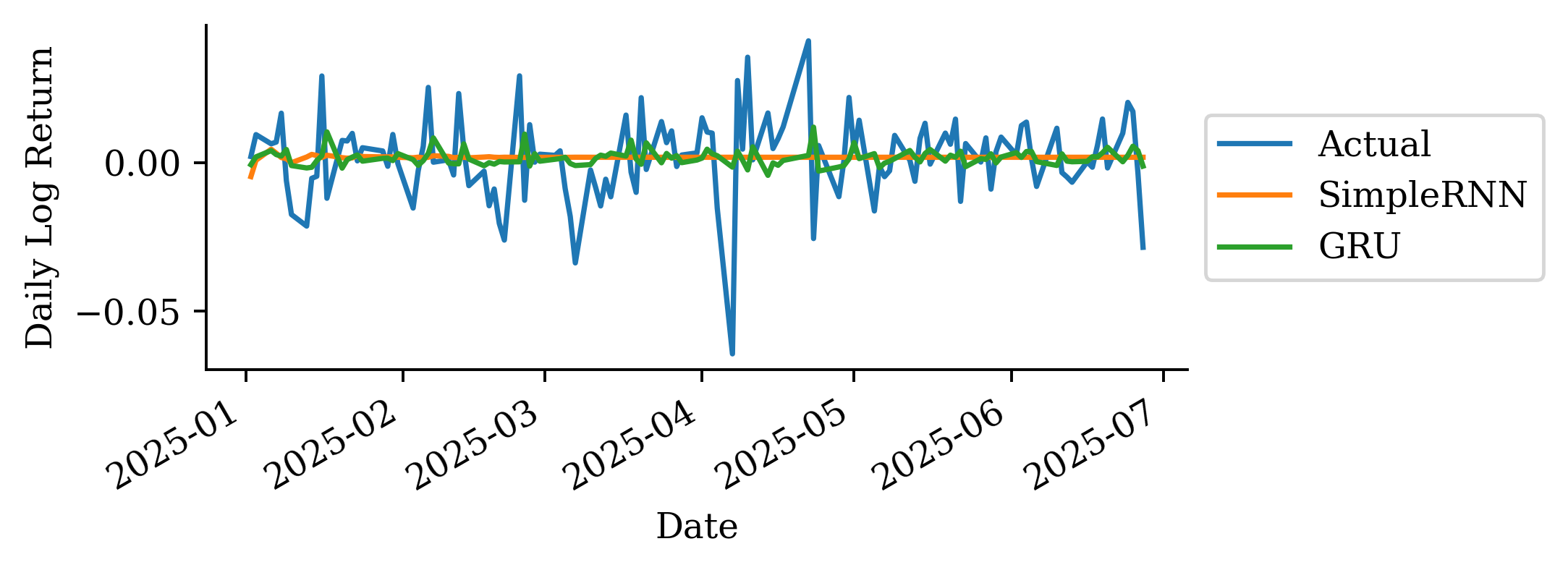
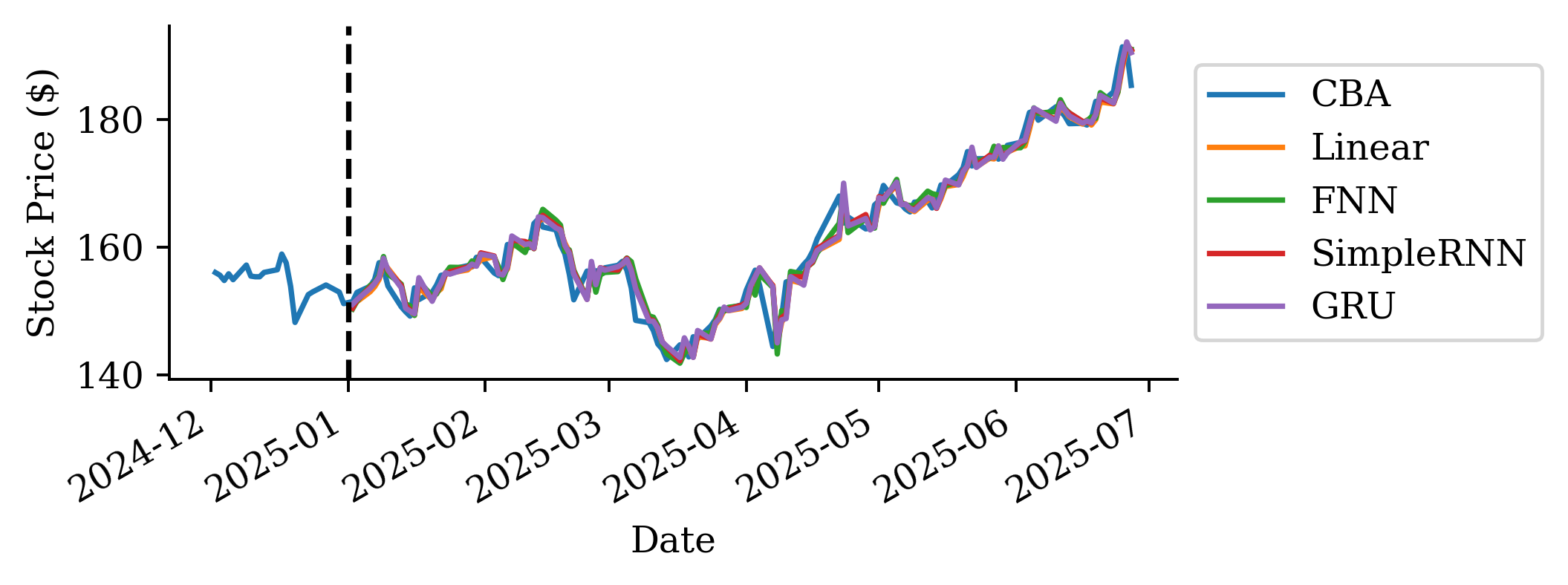
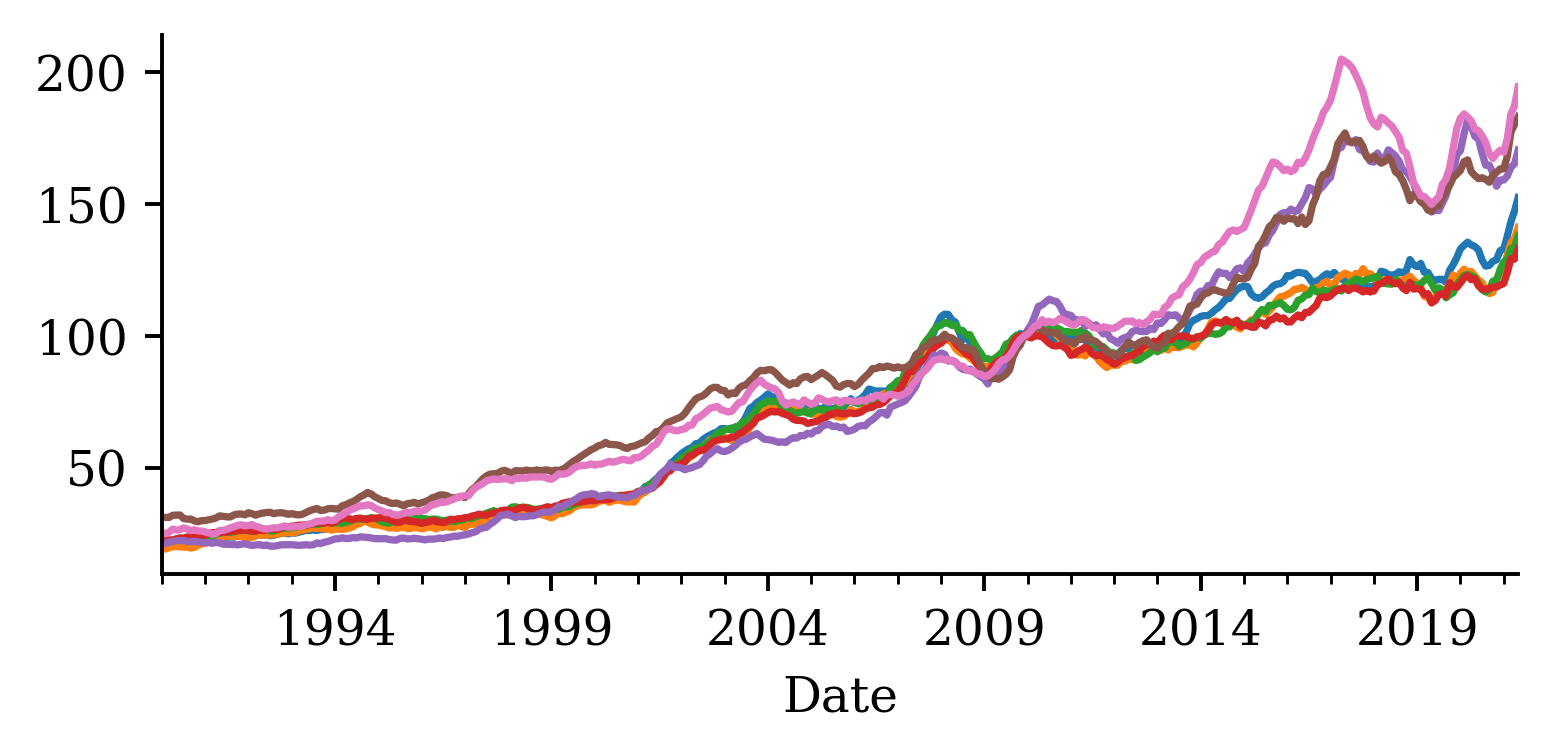
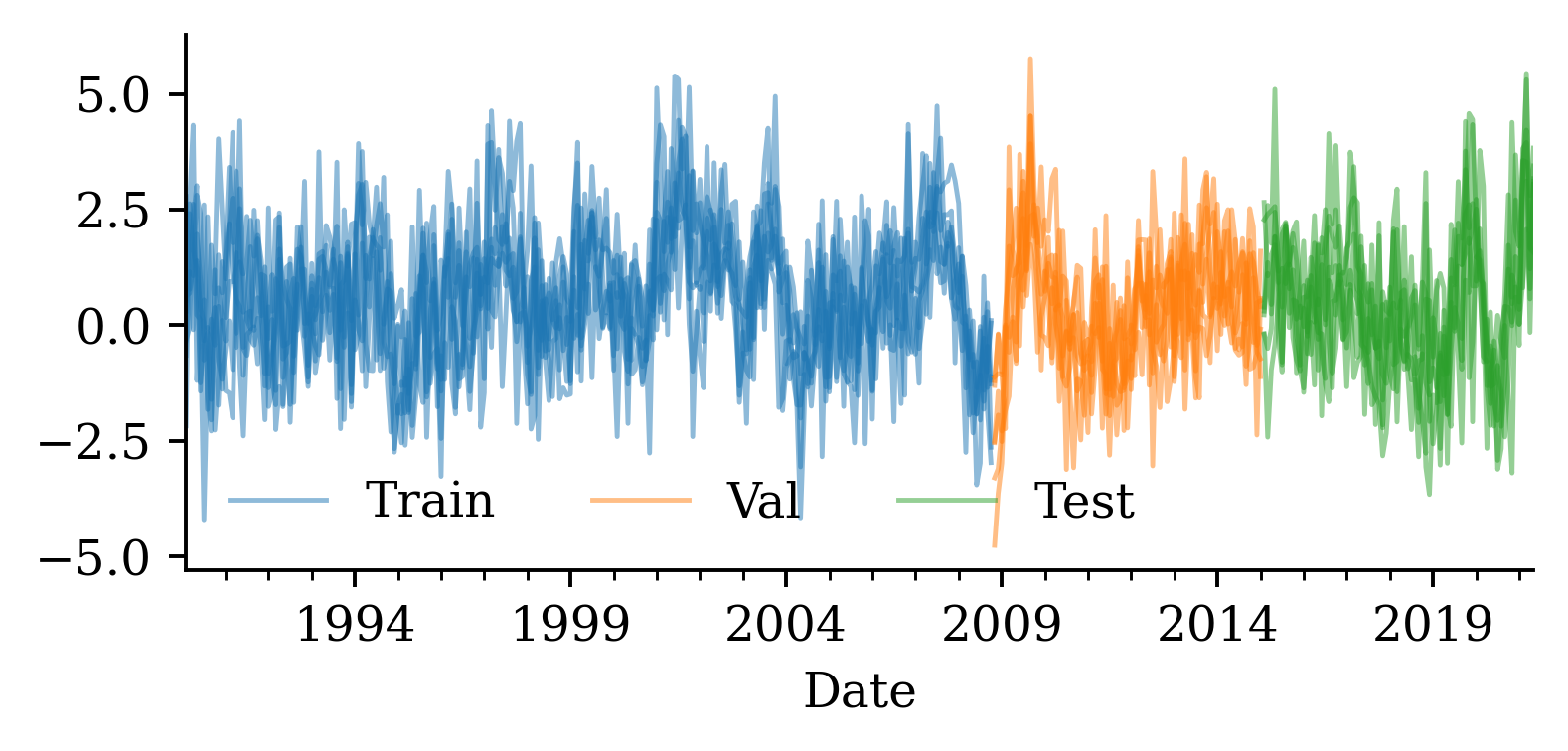
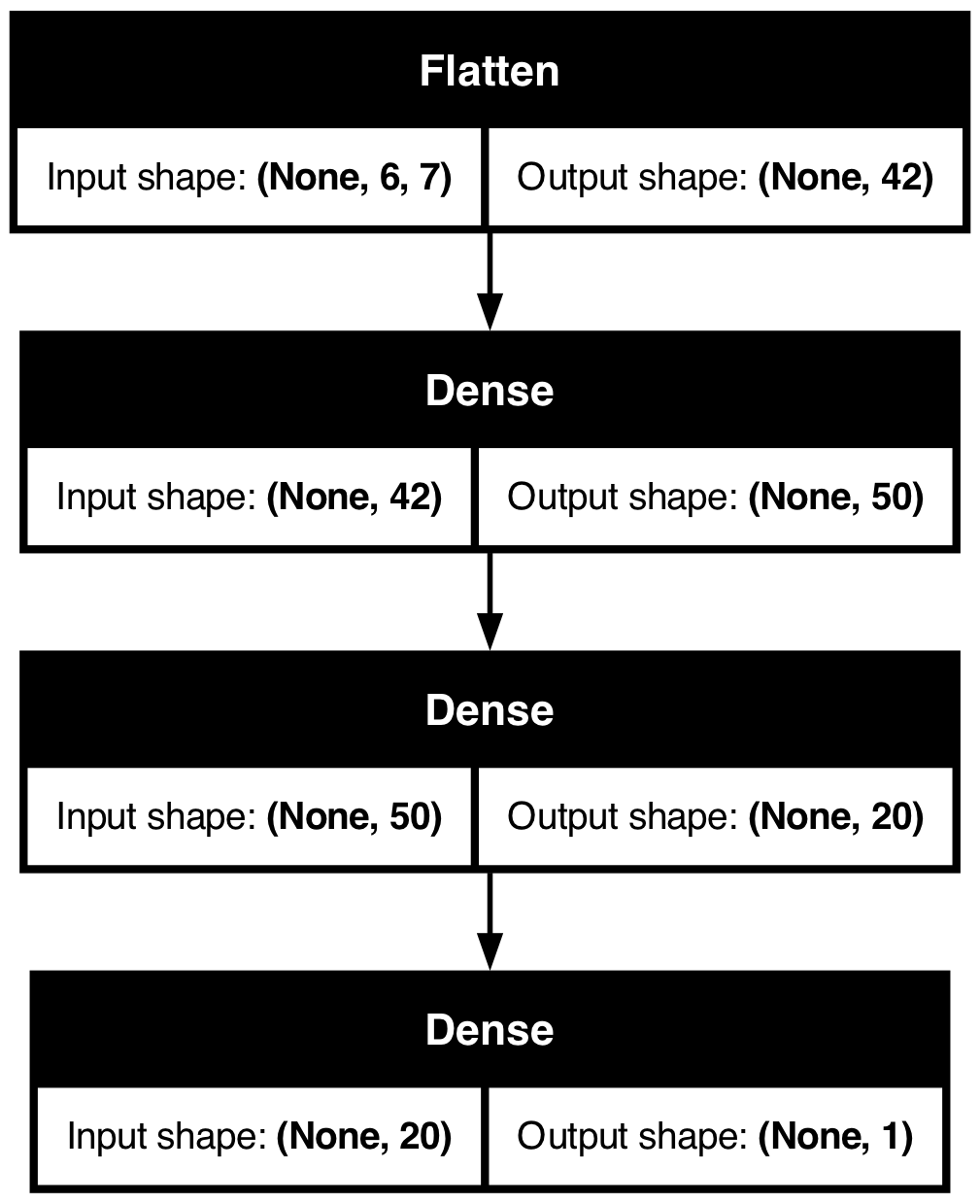
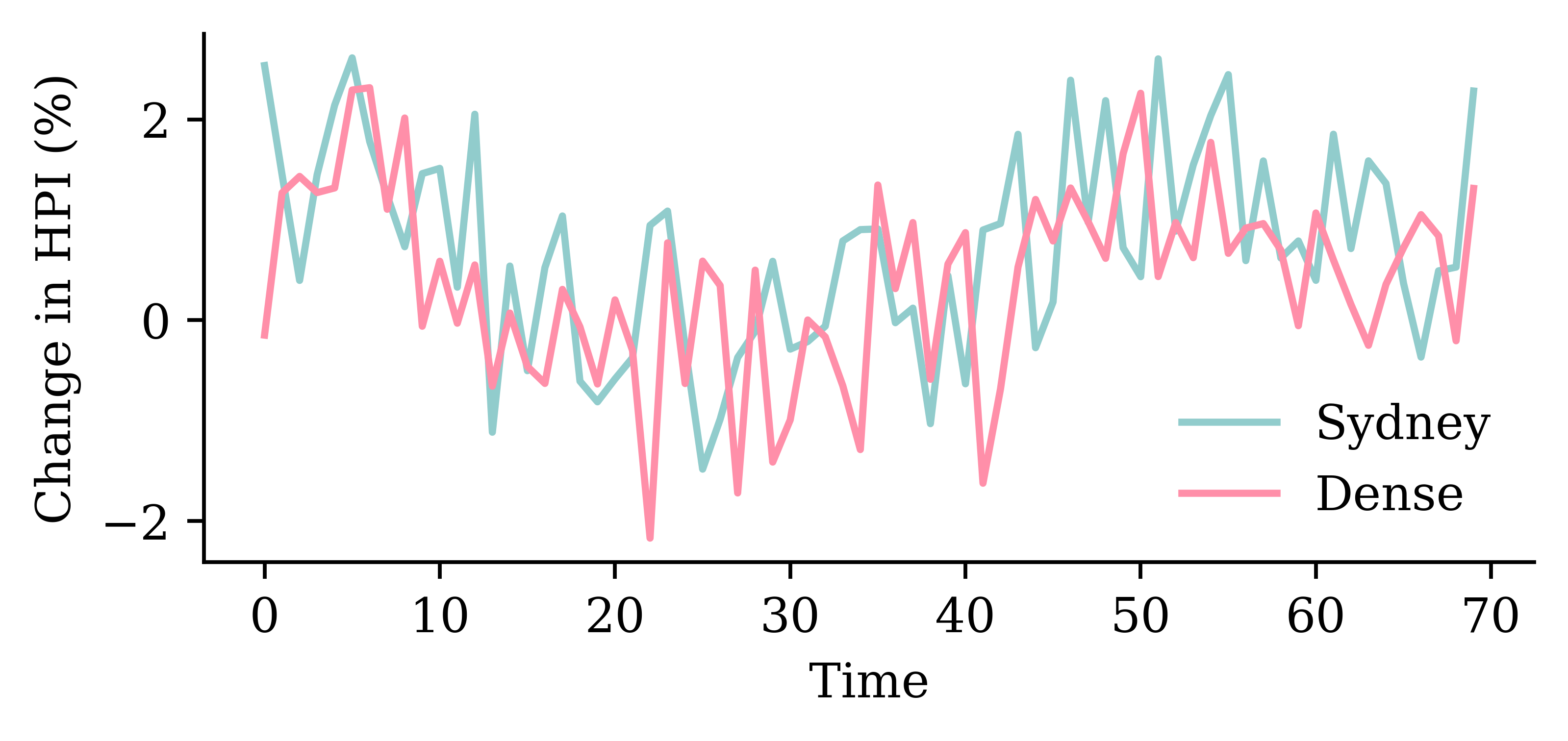
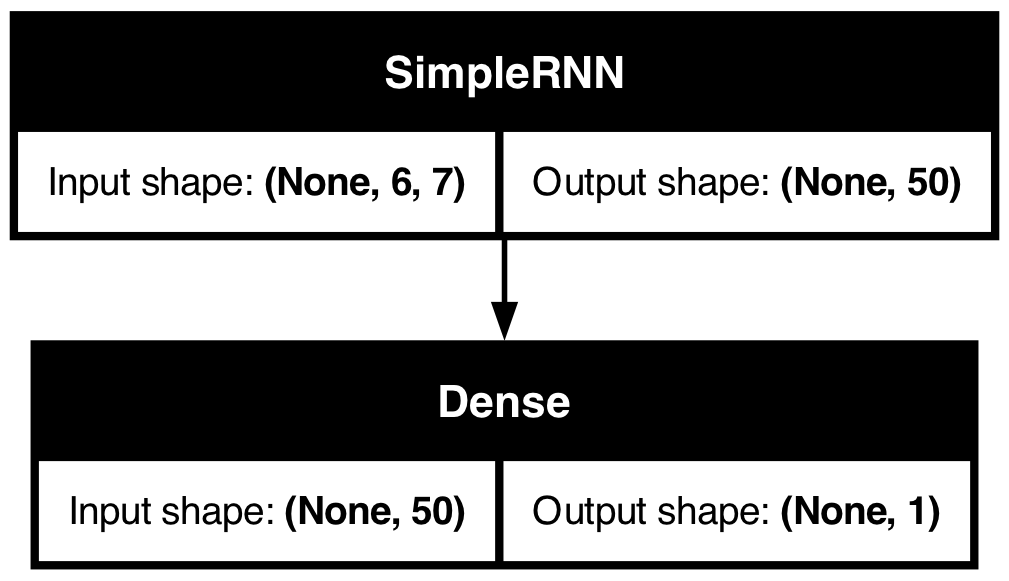
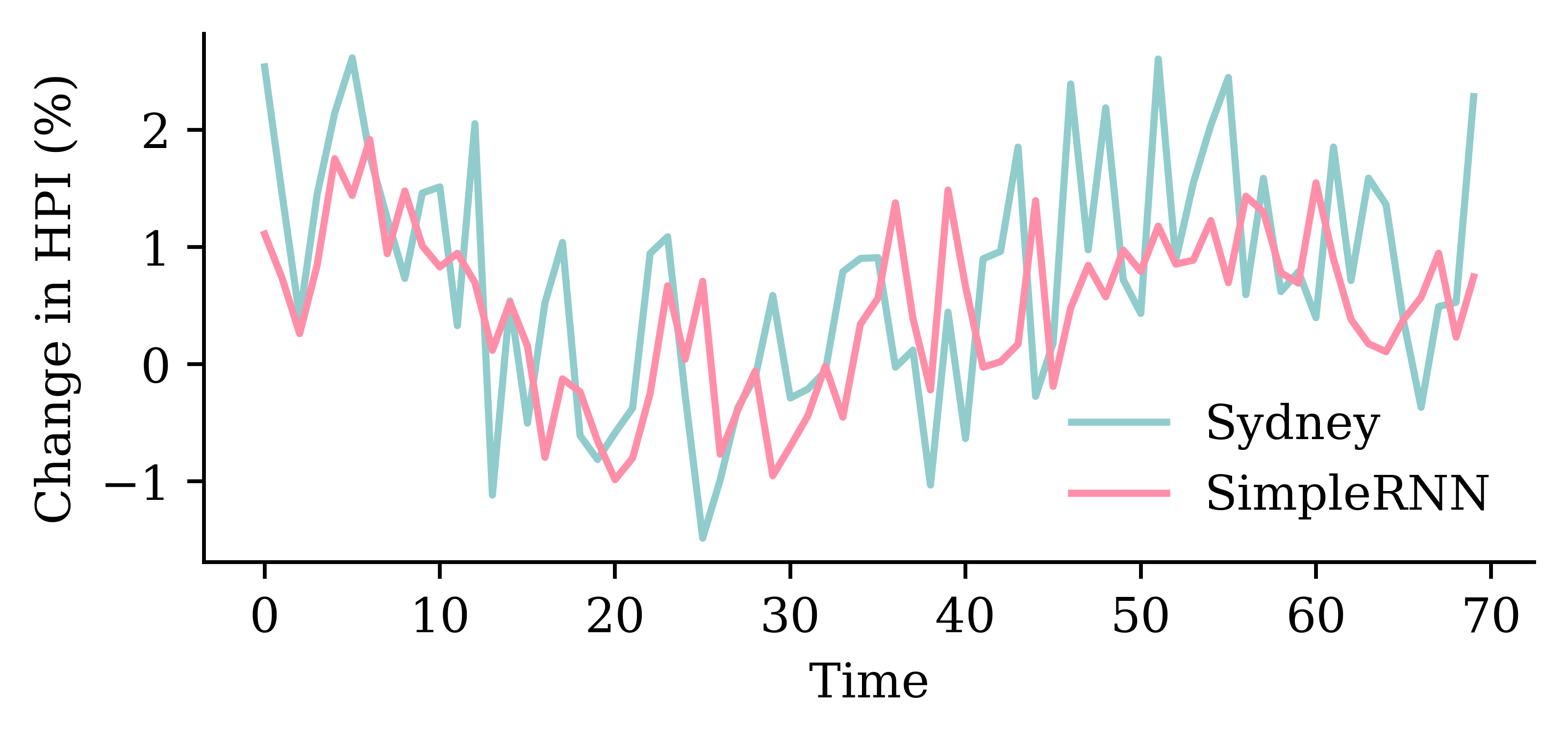
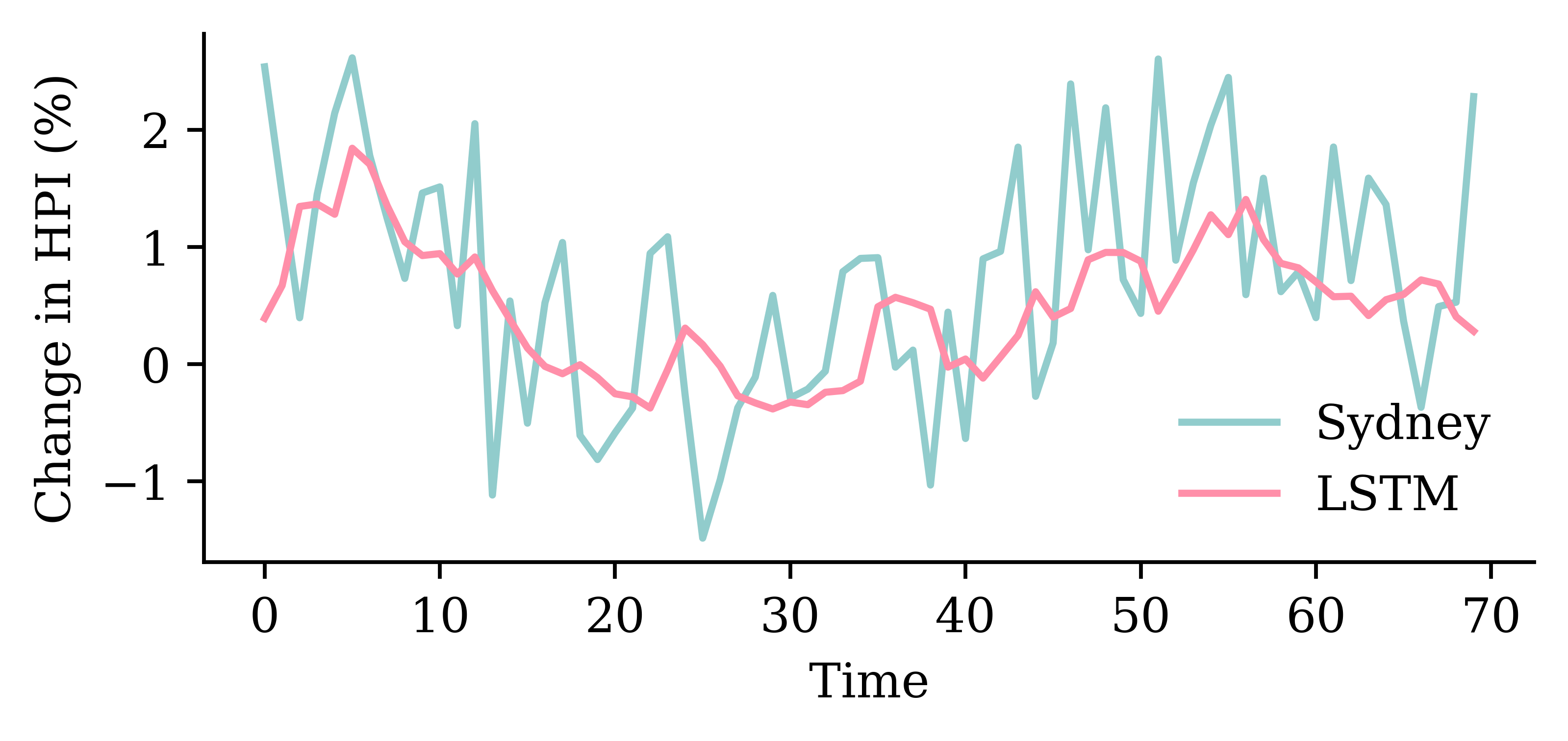
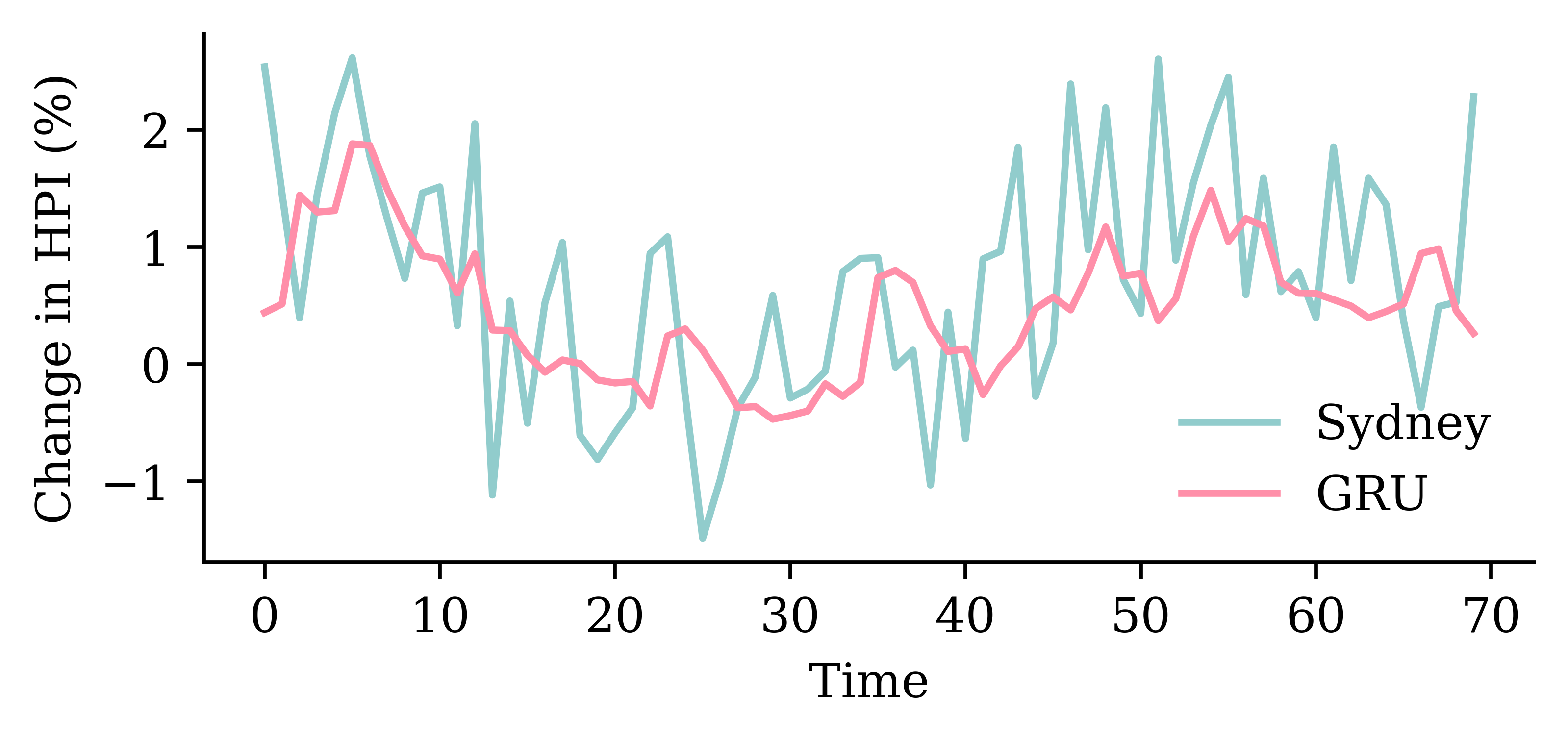
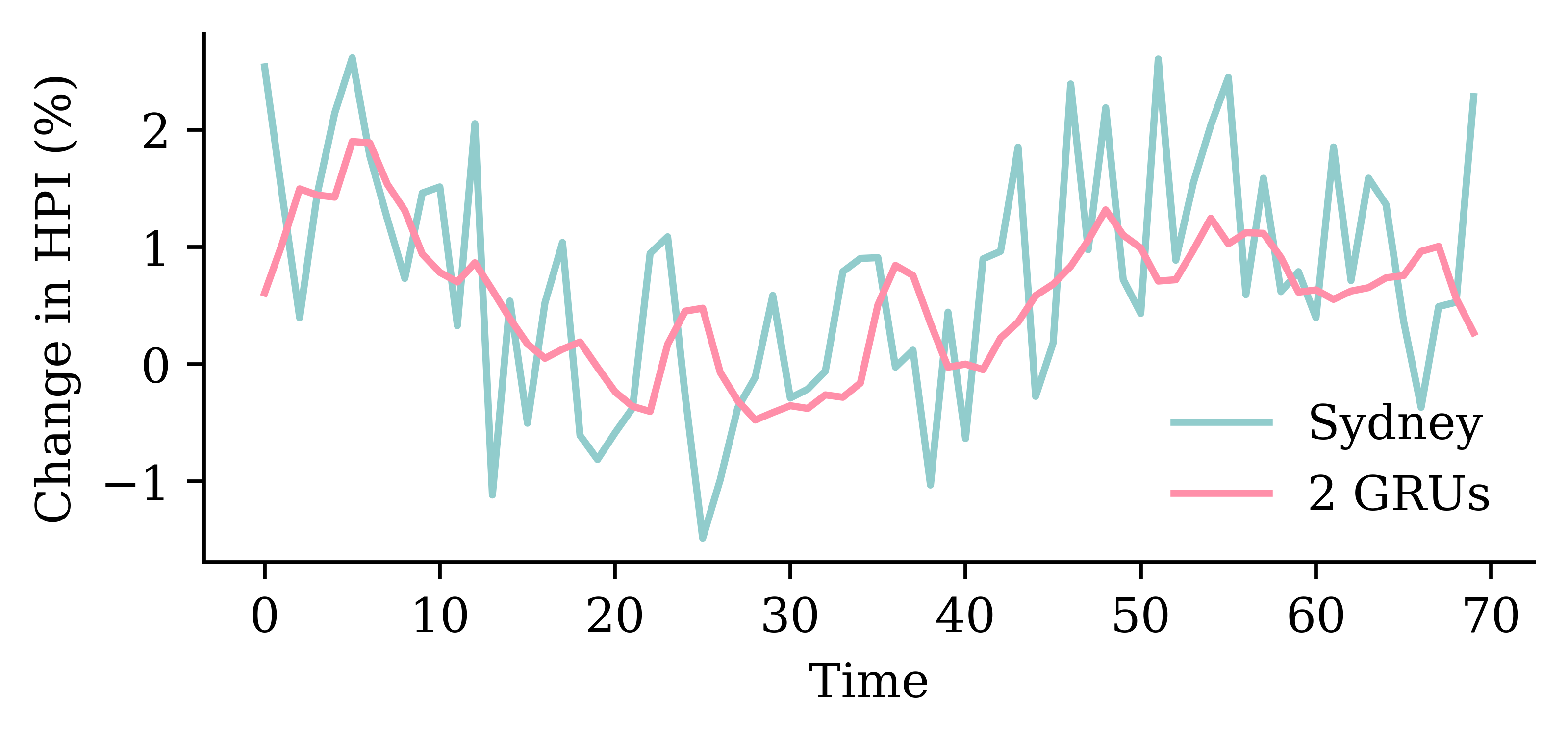
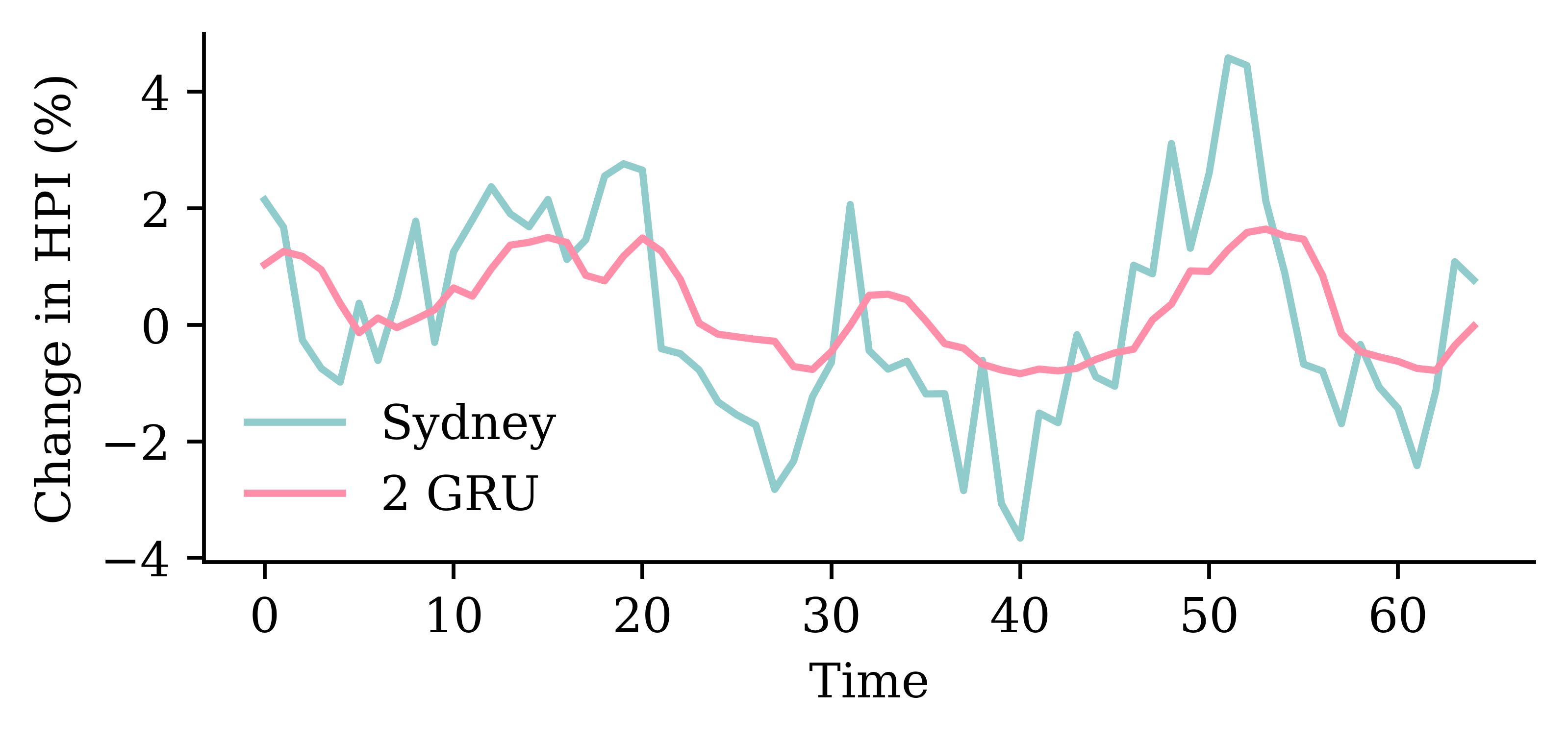
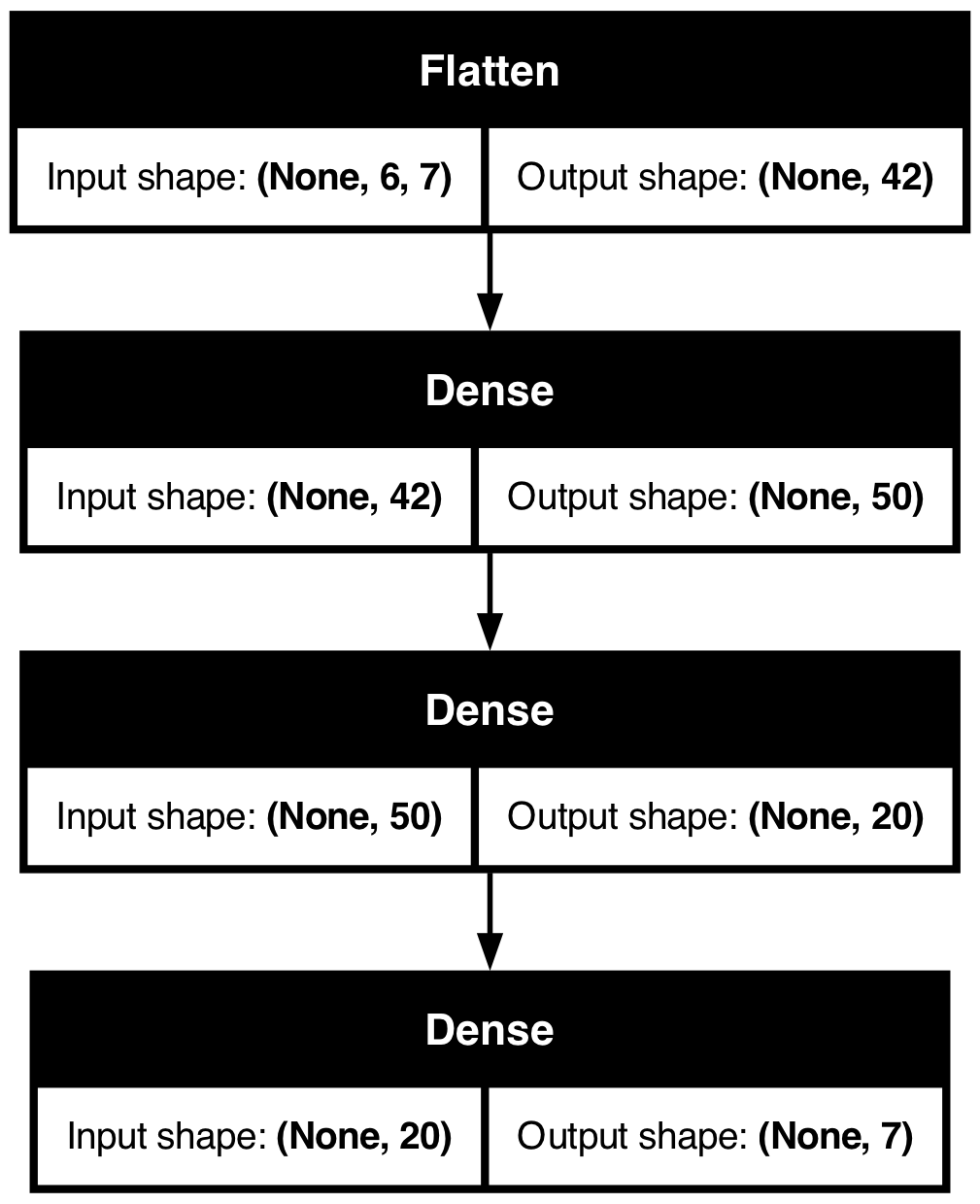
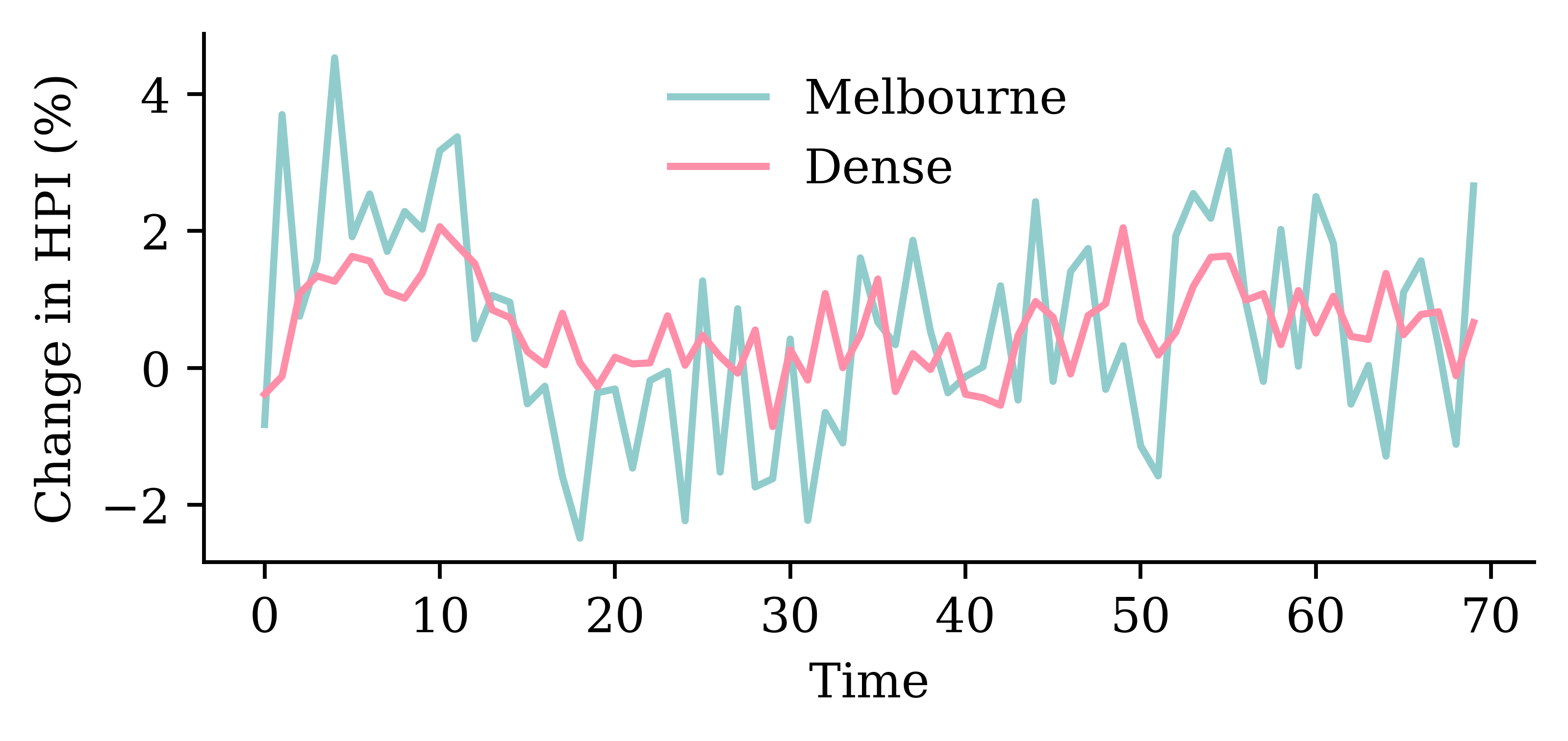
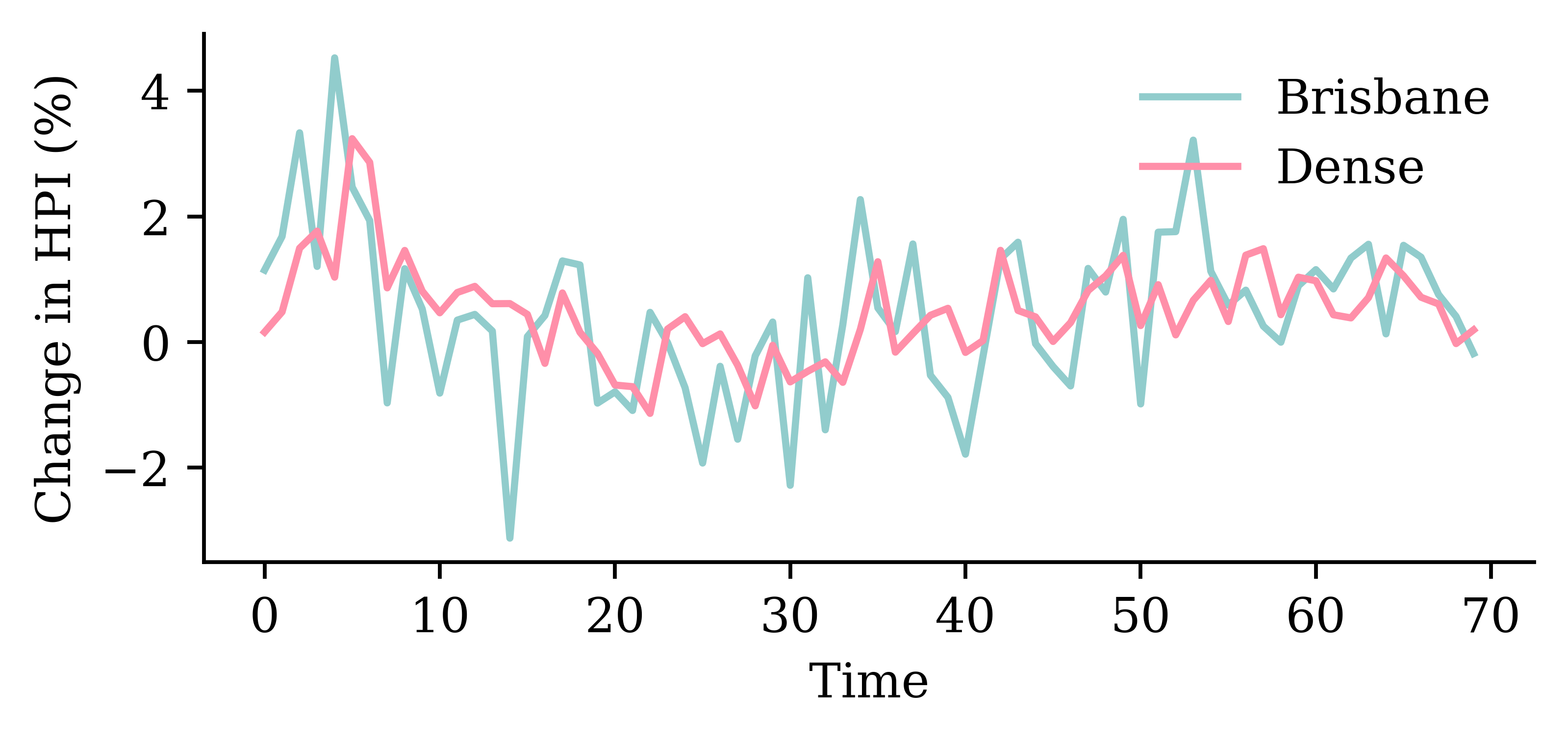
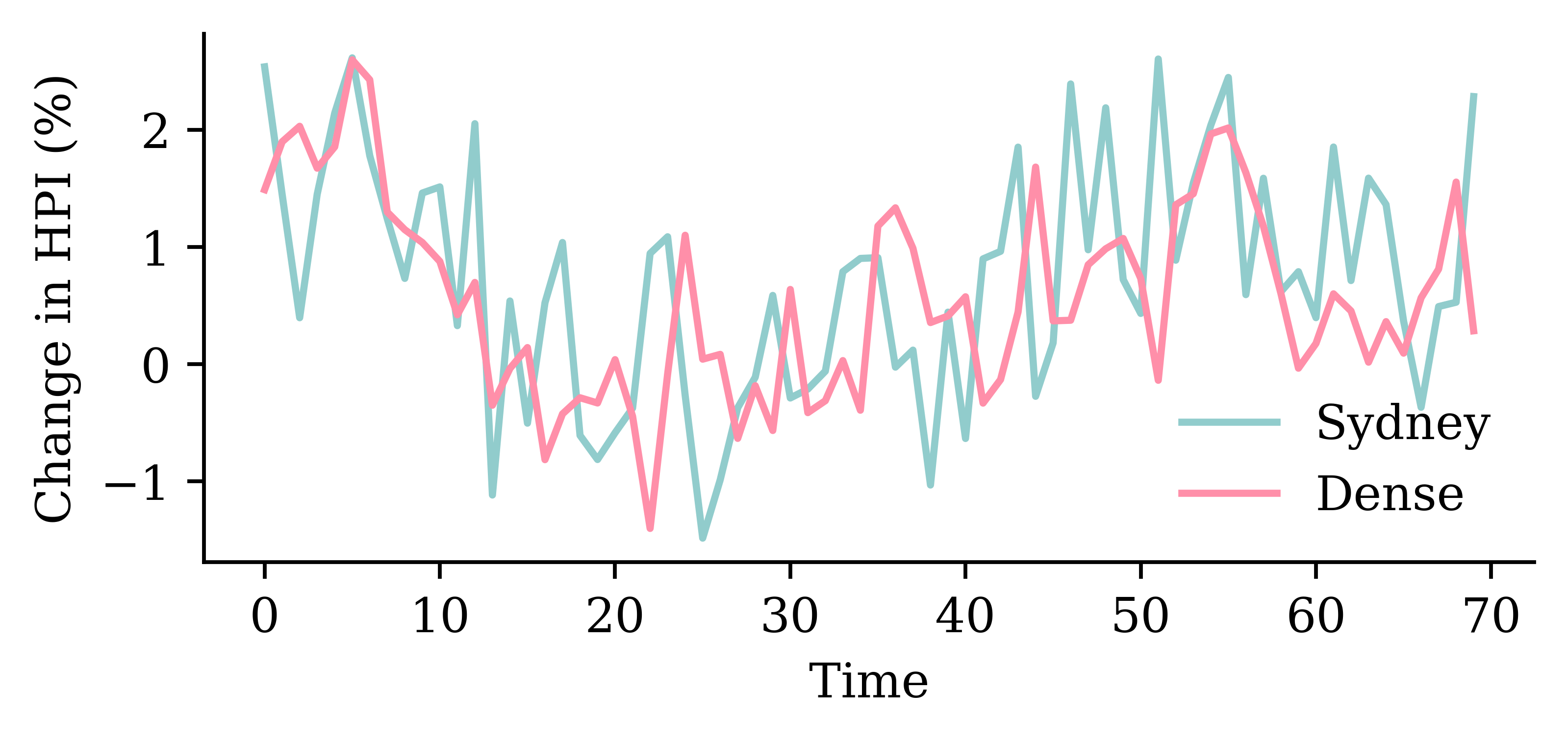
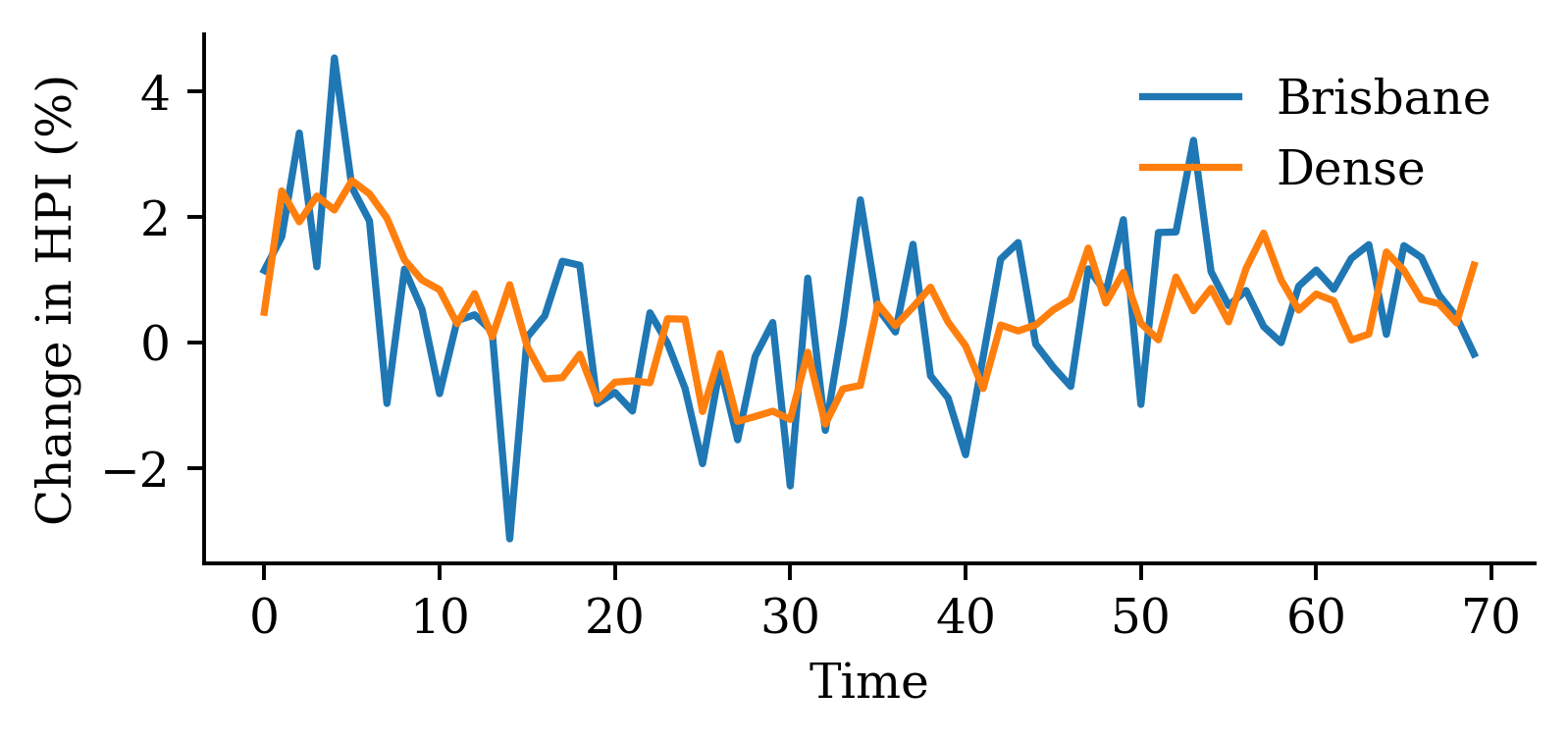
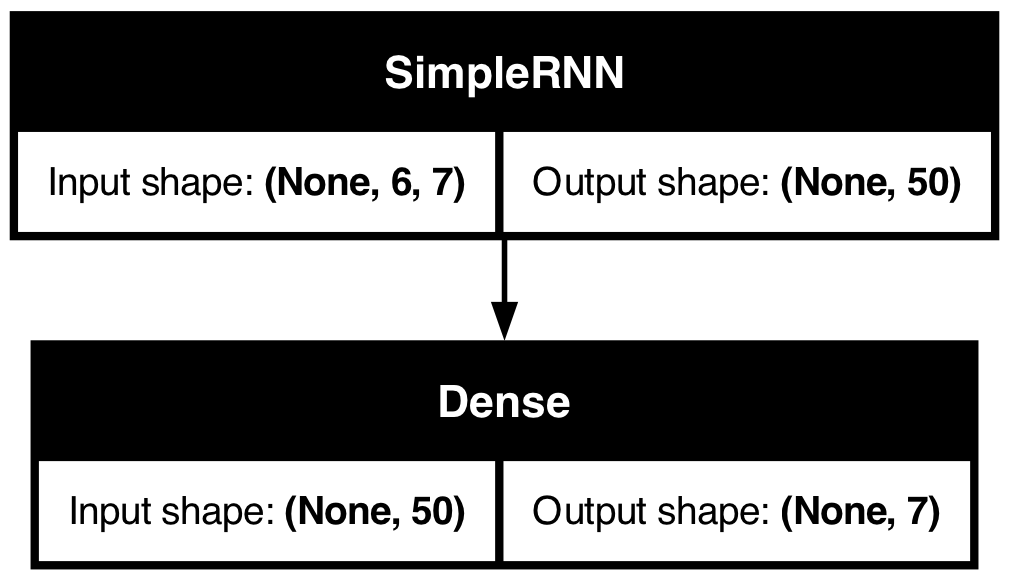
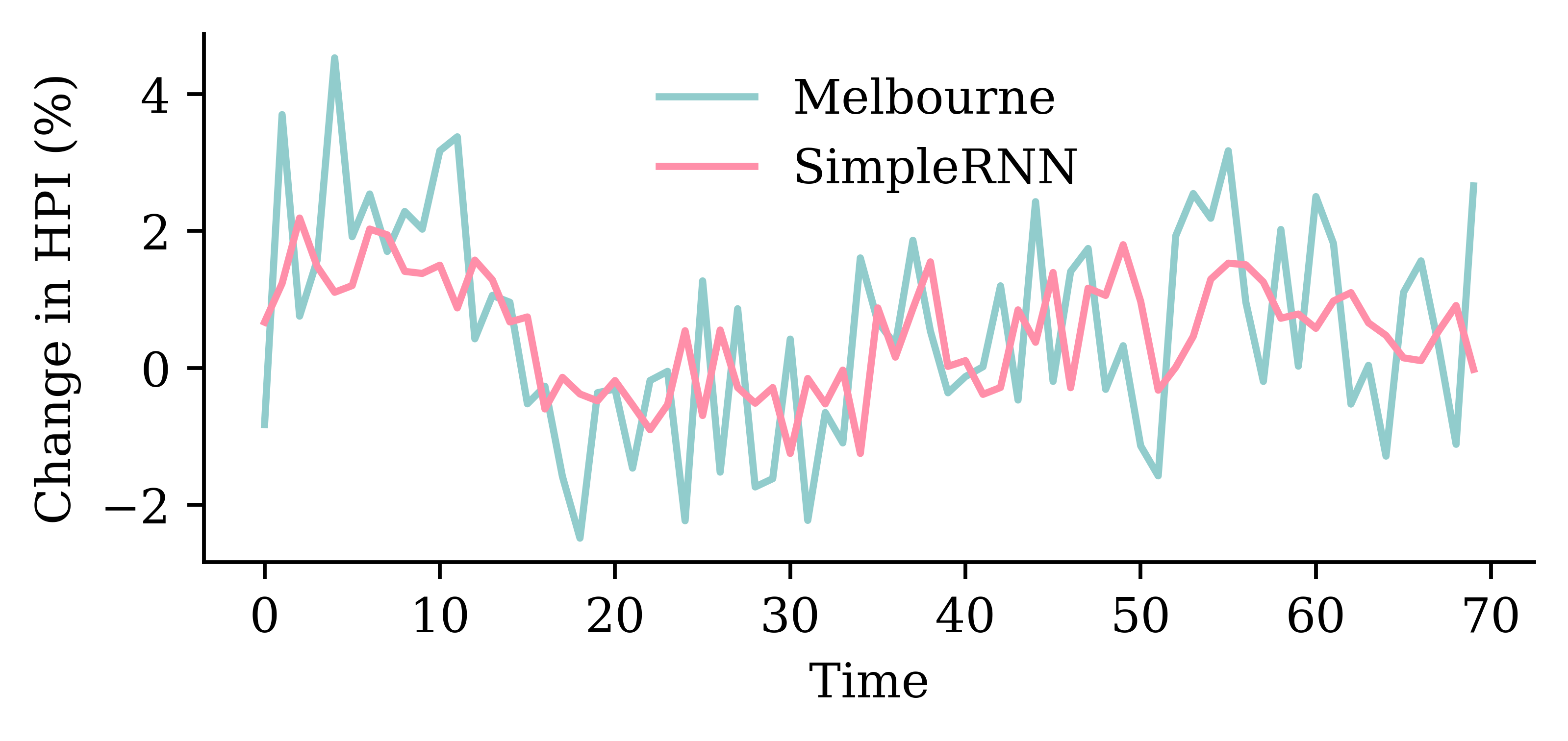
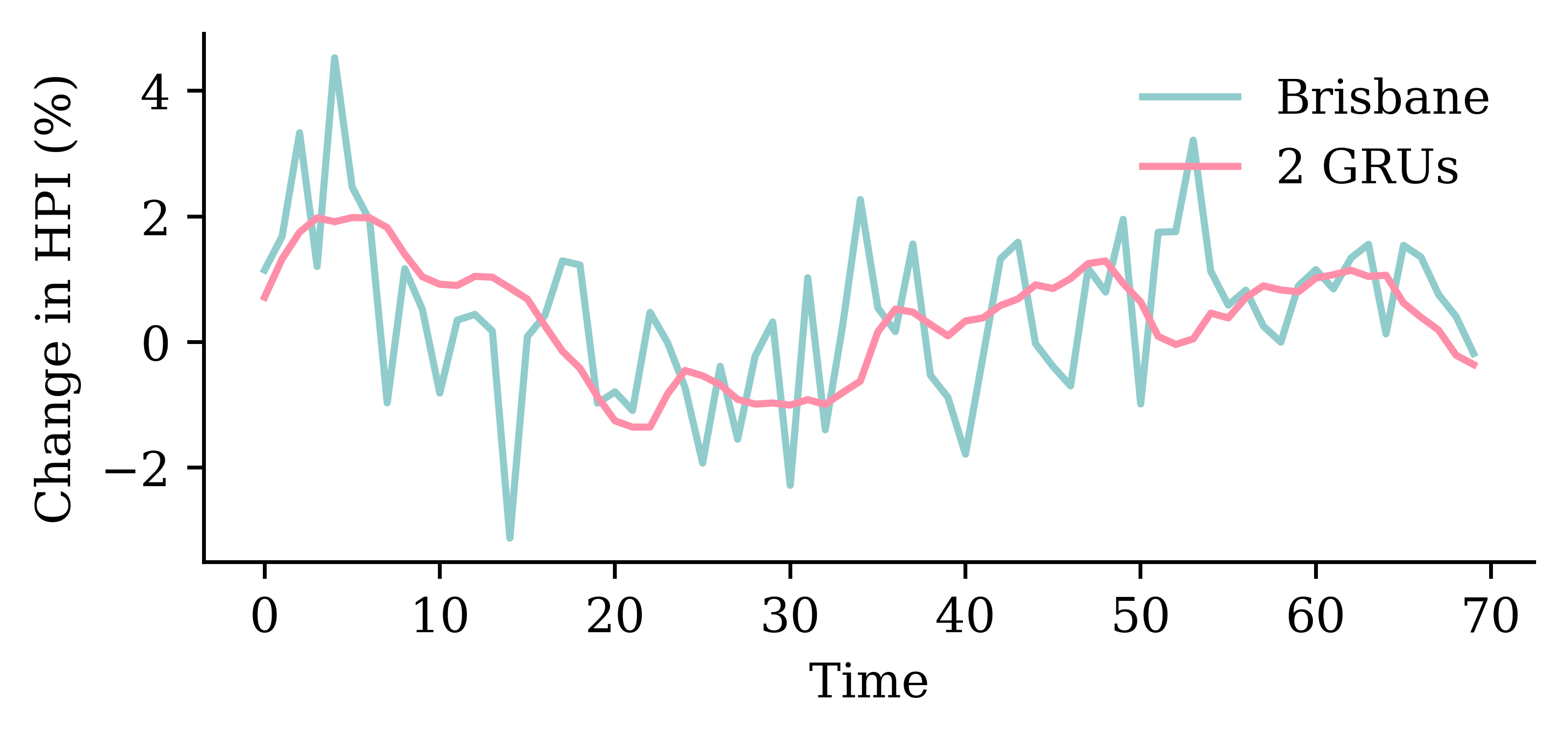
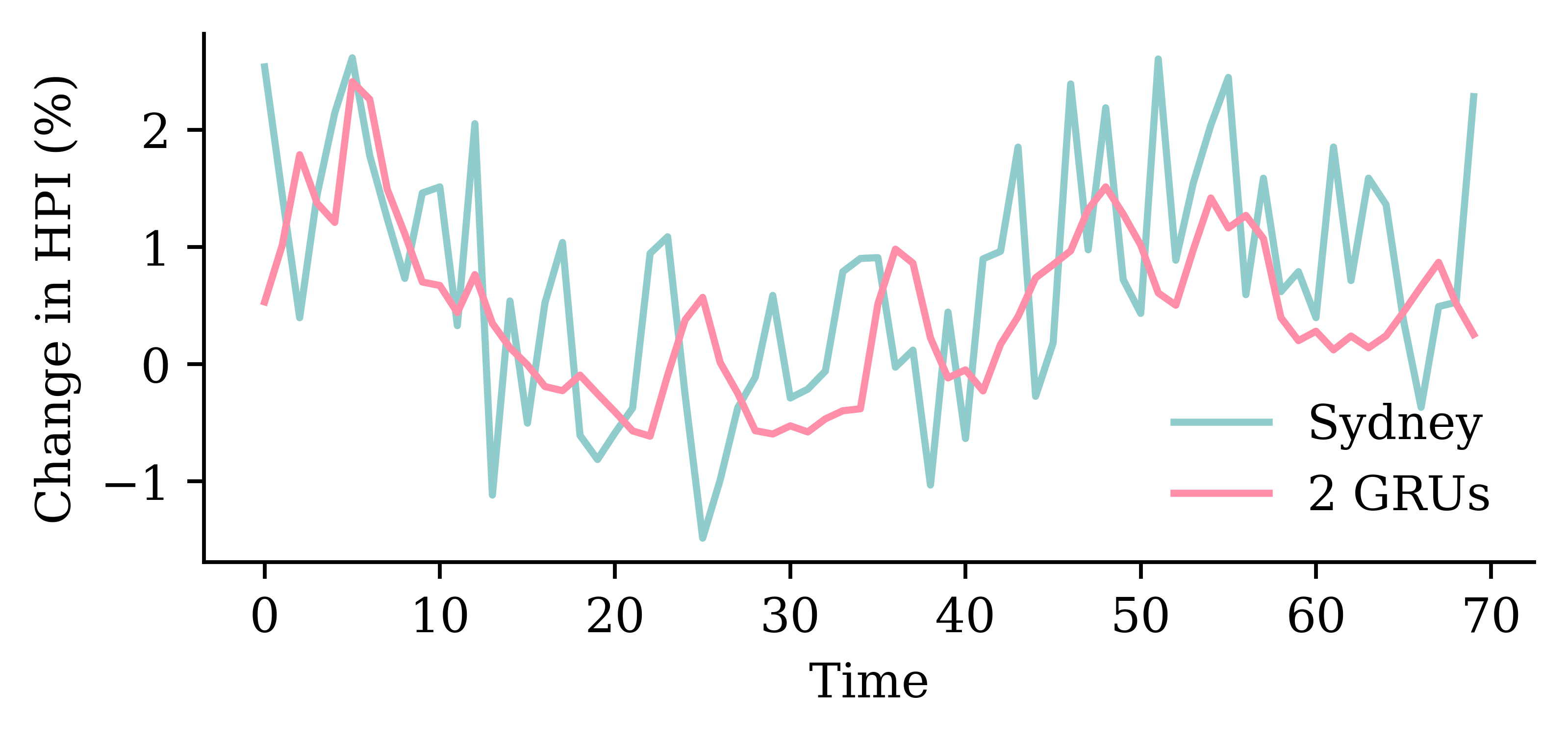
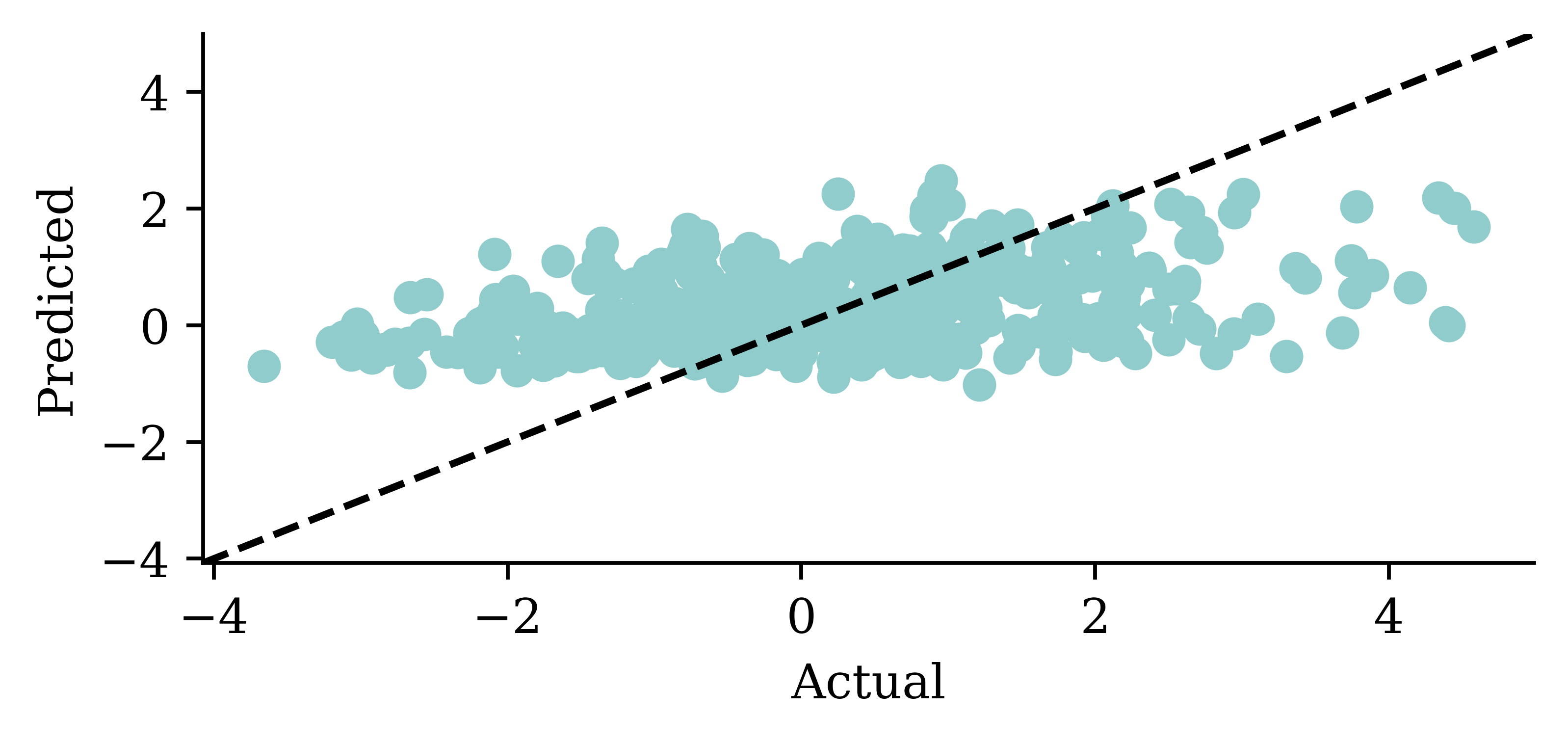
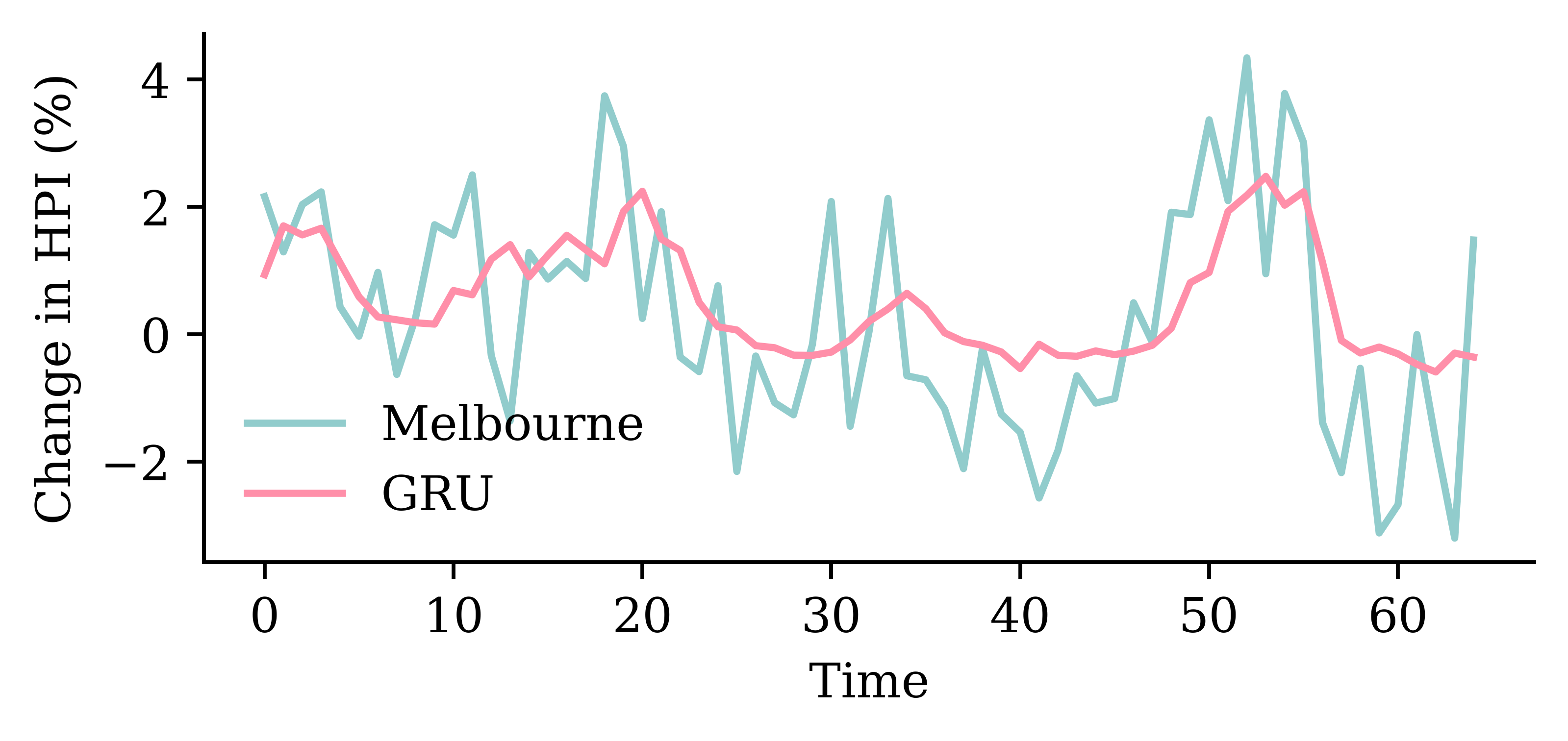
| Date | ANZ | ASX200 | BOQ | CBA | NAB | QBE | SUN | WBC | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1999-01-01 | 8.413491 | NaN | NaN | 14.560169 | NaN | NaN | 7.965791 | NaN |
| 1 | 1999-01-04 | 8.476515 | 2732.199951 | NaN | 14.402927 | 12.995510 | 2.648447 | 7.965791 | 6.370629 |
| 2 | 1999-01-05 | 8.452881 | 2716.600098 | NaN | 14.409224 | 13.169948 | 2.564247 | 7.965791 | 6.485921 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 6742 | 2025-06-25 | 29.100000 | 8559.200195 | 7.86 | 191.399994 | 40.049999 | 23.480000 | 21.750000 | 34.540001 |
| 6743 | 2025-06-26 | 29.740000 | 8550.799805 | 7.86 | 190.710007 | 39.889999 | 23.330000 | 21.459999 | 34.570000 |
| 6744 | 2025-06-27 | 29.200001 | 8514.200195 | 7.77 | 185.360001 | 39.259998 | 23.219999 | 21.330000 | 33.900002 |
6745 rows × 9 columns